Introducción

 

En la segunda mitad de la década de los ochenta, México emprendió un programa de estabilización y reforma económica que tenía como objetivo fundamental la reducción de la inflación. Después de una reducción drástica de la tasa de inflación, de 159 % en 1987 a alrededor de 20 % en 1991, el gobierno mexicano decidió mantener una tasa de cambio fija del peso mexicano con respecto al dólar. Mientras la tasa de cambio nominal permaneció constante, de 1990 en adelante, la inflación en México resultó ser más elevada que en los Estados Unidos provocando que los productos mexicanos fueran 22 % más caros que sus similares norteamericanos impactando de forma negativa en la balanza comercial mexicana (incremento del déficit comercial); de ahí que un país de ingreso medio como México debería confrontar grandes problemas financieros con tales niveles de déficit comercial. El supuesto teórico de una movilidad perfecta del capital que plantea que en la medida en que la tasa de interés interna sea igual a la tasa de interés externa los flujos de capital externos deben ser suficientes para financiar cualquier déficit, no es totalmente aplicable, aún para los países ricos.

En el caso de México, el financiamiento del déficit condujo a un excesivo incremento en las tasas de interés. Este hecho, no significó ningún tipo de problema  para México por lo menos hasta 1994. Sin embargo, durante el propio año 1994 la sobrevaloración del peso mexicano se convirtió en un problema bastante serio para los economistas estudiosos de la economía mexicana que consideraban a la devaluación como un hecho inevitable. Para diciembre de ese año, el miedo a una posible devaluación provocó la salida de grandes flujos de capital y por tanto el peso mexicano se vio devaluado en un 50 %. Un año después, en diciembre de 1995, la cotización era de 7,75 pesos por dólar estadounidense comparado con el valor de 3,45 pesos por dólar estadounidense que había en noviembre de 1994.

La razón por la cual la devaluación del peso mexicano fue tan profunda es que la mayoría de los inversionistas extranjeros decidieron salir de México al unísono. Aquellos, que permanecieron en el país, exigieron a cambio altas tasas de interés; las tasas de interés nominales a corto plazo promediaron 50% de enero a diciembre del 1995. Paradójicamente, este fenómeno ocurrió acompañado con una inflación galopante. Estimados preliminares realizados, plantean que en 1995 el PIB de México disminuyó cerca del 10% debido principalmente a las altas tasas de interés existentes y no a los efectos de la devaluación del peso mexicano.

En el trabajo emplearemos un modelo de competencia imperfecta que relaciona el índice de concentración [1] con el desempeño industrial medido a través de la variable, que representa el margen neto de utilidades con respecto a las ventas, con la intención de analizar, desde el punto de vista microeconómico, el impacto que tuvo la crisis de diciembre del 94 sobre el desempeño industrial mexicano.      

Fundamento Teórico:

 

Teóricamente, se puede plantear el siguiente modelo microeconómico:

Si el beneficio de una empresa  de una determinada industria viene dado por la expresión:

Donde:

: representa la curva de demanda inversa del mercado.

: representa la producción total de la industria.

Entonces, la condición de primer orden para la maximización del beneficio de la empresa  es:

Donde:

: representa la producción combinada de todas las empresas excepto de la empresa . Es decir,

Si la empresa  trata la derivada conjetural  como una constante, entonces se puede obtener el índice de Lerner específico de la empresa .

 

Donde:

: Porción del mercado dominada por la empresa .

: representa la elasticidad precio de la demanda por la industria.

De manera que el poder de mercado de la empresa (representada por el índice de Lerner específico de la empresa) depende de la porción de mercado dominada por la empresa y de las expectativas de la empresa acerca de la conducta de las empresas rivales.

Si tomamos un promedio ponderado de los índices de poder de mercado específico de las empresas, usando las porciones de mercado como pesos específicos, se obtiene un índice de Lerner promedio de la industria.

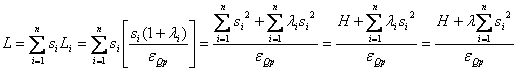
……………………………………………………………… (1)

Donde:

: representa el índice de concentración de Herfindahl[2].

Si se trata la elasticidad conjetural de la empresa  ,  igual a una constante, se obtiene:

En el caso del índice de Lerner promedio de la industria.

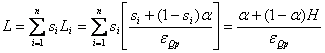 …………………. . … (2) 

Por otro lado, si se supone que la industria está dominada por un grupo de  empresas, con el resto de  empresas tomadoras de precio[3], en las que el índice de Lerner es igual a cero

El grupo dominante selecciona los diferentes valores de , para , con el objetivo de maximizar la siguiente función de beneficio:

 

 

Donde:

: representa el producto generado por el grupo dominante.

: representa el producto generado por el resto del grupo.

Si el grupo dominante mantiene una derivada conjetural , que expresa la respuesta del resto de grupo a los cambios en el producto del grupo dominante, constante.

Entonces, la condición de primer orden en la maximización del beneficio con respecto a  es:

Si se supone que el costo marginal es el mismo para todos los miembros del grupo dominante e igual a , entonces el índice de Lerner para el grupo dominante es:

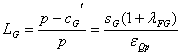
Luego, el índice de poder de mercado promedio de la industria es:

 

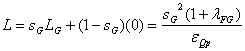
Si se considera que el grupo dominante mantiene una elasticidad conjetural constante  con respecto a la respuesta del resto del grupo a cambios en el nivel de producto del grupo dominante, se puede expresar el índice de Lerner promedio de la industria de la siguiente forma:

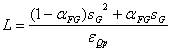…………………………………………………(3)

Donde:

: representa el índice de concentración () para el grupo de  empresas dominantes[4].

En ambos casos, el desarrollo teórico muestra como el índice de concentración de Herfindahl y el índice de concentración () están relacionados estructuralmente con el índice de Lerner de poder de mercado a nivel de industria.

 

 

 

También es posible plantear a nivel de industria que:

Beneficios o Utilidades

Ventas

Entonces:

Rendimiento (índice de poder de mercado)

 El rendimiento representa en sí una medida indirecta del poder de mercado[5].

Luego, el establecimiento de una relación entre el rendimiento y los índices de concentración a nivel de industria, es factible desde el punto de vista teórico. En estudios anteriores realizados en el ámbito de la industria manufacturera[6], se obtuvieron algunos modelos matemáticos lineales, al relacionarse los índices de concentración vistos arriba con respecto a dos tipos de variables de desempeño: una representada por el margen existente entre el precio y el costo, y la otra por el margen neto de las utilidades con respecto a las ventas. De ahí que el modelo propuesto sea totalmente valido para su aplicación

Por otra parte, uno de los criterios más importantes que se deben considerar en una ecuación es la de tener relevancia fuera del conjunto muestral empleado en la estimación. Este criterio se fundamenta en la noción de constancia paramétrica. Es decir, que la ecuación puede ser aplicada tanto dentro como fuera del conjunto muestral. Esta constancia paramétrica, puede ser probada por diferentes vías siendo una de las más empleadas, las pruebas de precisión predictiva. En el trabajo, se aplicará la prueba de Chow para validar la constancia de los parámetros dentro del modelo de competencia imperfecta adoptado.

Prueba de Chow[7]

Esta prueba consta de los siguientes pasos:

1.                 Usando las  observaciones designadas, se obtiene el modelo no restringido, el cual tiene asociado una suma de cuadrados no restringida .

2.                 Usando todas las observaciones , se obtiene el modelo restringido, el cual tiene asociado una suma de cuadrados restringida .

3.                 Se calcula el valor del estadígrafo 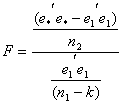  rechazándose la hipótesis de constancia de los parámetros en el caso de que exceda a un valor crítico preestablecido.

 

 

Resultados y discusiones

 

Precisamente, aplicaremos esta prueba para analizar la variación del modelo de desempeño en el período comprendido entre los años 1994 y 1996.

Se toman los datos sectoriales de desempeño de los años 1994 y 1995 en conjunto y se le ajusta un modelo del tipo

 

 

Tabla 1 Parámetros del modelo

Nota: obtenida utilizando el paquete computacional STATGRAPHICS PLUS,  a partir de los

datos de las Tablas 6 y 7  

 

Tabla 2 Análisis de Varianza del modelo

Nota: obtenida utilizando el paquete computacional STATGRAPHICS PLUS, 

a partir de los datos de las Tablas 6 y 7.

 

La ecuación del modelo fijado es:

……………………….(4)

Ya que el p-value en la tabla 2, es menor que 0.05, entonces hay una relación estadísticamente significativa entre  y  con un intervalo de confianza del 95%. Debido a que valor de p-value del intercepto es mayor que 0,05 (ver Tabla 1), entonces podemos eliminar el intercepto del modelo con un nivel de confianza mayor que 95%.

Considerando:

Suma de cuadrados restringida = 59554,80

Suma de cuadrados no restringida [10]= 2538,66

Aplicando la Prueba de Chow tenemos:

=  =

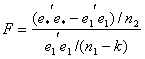De la tabla de la distribución F: [11]

 Se rechaza la hipótesis nula, por lo que no hay constancia en los parámetros del modelo al pasar del año 1994 al año 1995.

Si se toman los datos sectoriales de desempeño de los años 1995 y 1996 en conjunto, y se le ajusta el mismo modelo se obtiene.

 

Tabla 3 Parámetros del modelo

Parámetro	Estimado	Error	T	p-Value
Intercepto (a) Pendiente (b)	-52,6808 16,6765	39,7405 5,0902	-1,3256   3,2762	0,1914 0,0020

Nota: obtenida utilizando el paquete computacional STATGRAPHICS PLUS, 

a partir de los datos de las Tablas 7 y 8

 

Tabla 4 Análisis de Varianza del modelo

Fuente	SC	g.l	Cuadrado Medio	F-Ratio	p-Value
Modelo Residuos	24 366,6 106 699,4	1 47	24 366,6 2 270,2	10,73	0,0020
Total	131 066,0	48

Nota: obtenida utilizando el paquete computacional STATGRAPHICS PLUS,  a partir de los datos

de las Tablas 7 y 8

 

La ecuación del modelo fijado es:

……………..(5)

Ya que el p-value en la tabla 4 es menor que 0.05, entonces hay una relación estadísticamente significativa entre  y  con un intervalo de confianza del 95%. Debido a que valor de p-value del intercepto es mayor que 0,05, entonces podemos eliminar el intercepto del modelo con un nivel de confianza de al menos 95 %.

Considerando:

Suma de cuadrados restringida = 106699,4

Suma de cuadrados no restringida [12]= 46545,0

Aplicando la Prueba de Chow tenemos:

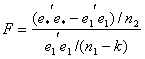== 0,94

De la tabla de la distribución F: [13]

 No se rechaza la hipótesis nula por lo que hay constancia de los parámetros en el modelo al pasar del año 1995 al año 1996.

De ahí que podamos describir el modelo de desempeño en el período de 1995-1996, mediante la ecuación:

Conclusiones

 

La evaluación del cambio estructural en el período 94-96 aparece en tabla 5

 

Tabla 5 Evaluación del cambio estructural  en el período 94-96

Modelo conjunto	Parámetros del modelo[14]	Validez de [15]
1994-1995		No
1995-1996		Si

 

Los resultados de la tabla 5, muestran un cambio en el modelo existente a partir del año 1995 lo cual pudiera ser atribuible al hecho de que ante la evolución de la crisis, el gobierno mexicano se vio obligado a hacer una fuerte contracción de la demanda interna y una política monetaria restrictiva que originó incrementos en las tasas de interés, a niveles de entre 100% a 140%, lo cual repercutió negativamente en el desempeño de la industria mexicana, afectando de cierta forma el modelo de competencia que existía. Por otra parte, se aprecia de las tablas 1 y 3 que en las expresiones (4) y (5), el intercepto no es significativo mientras que la pendiente si lo es, lo cual corrobora la permanencia del poder de mercado en ambos períodos analizados.

 

REFERENCIAS

 

Chow, G. C. (1960), “Test of Equality between Sets of Coefficients in Two Linear Regressions”, Econometrica, 52, p 211-12.

Connolly, R. A, M. Hirschey (1984), “R&D, Market Structure and Profits: A value-based approach”, Review of Economics and Statistics, 6, p.678-681.

Johnston, J. (1997), “Econometric Methods”, 4th edition, New York: McGraw-Hill.

Revista EXPANSION (Julio-agosto 1995), México, p 458-83

___________________ (Julio-agosto 1996), México, p 482-505.

___________________ (Julio-agosto 1997), México, p 374-97.

Schmalense, Richard C. (1989), “Inter-industry studies of structure and performance”, Handbook of Industrial Organization, Vol II, Amsterdam: North-Holland, p 951-1009.

______________________ (1988), “Industrial Economics: An Overview”, Economic Journal, 98, p.643-681.

Torres Fernandez, Alfredo (2006), “El desempeño industrial como medida indirecta del poder de mercado”, Revista Comercio Exterior, Vol.56 (1).

 

 

 

 

 

 

 

 

 

 

 

 

 

Tabla 6. Desempeño industrial por sectores en el año 1994.

Nota: Revista EXPANSION (Julio-agosto 1995), México, pp 458-83

Tabla 7. Desempeño industrial por sectores en el año 1995.

Nota: Revista EXPANSION (Julio-agosto 1996), México, pp 482-505

 

Tabla 8. Desempeño industrial por sectores en el año 1996.

Nota: Revista EXPANSION (Julio-agosto 1997), México, pp 374-97