
Revista académica de economía
con
el Número Internacional Normalizado de
Publicaciones Seriadas ISSN
1696-8352
ANÁLISE ECONOMÉTRICA DA DEMANDA DE CARNE DE FRANGO A PARTIR DO EVIEWS 3.0
Azael de Souza Ribeiro
Daniel Meireles de Amorim
Flávio Sabathé Vera
Niels Kim da Silva Tahara
Heriberto Wagner Amanajás Pena (CV)
heripena@yahoo.com.br
Resumo
Neste trabalho determinou-se a estimação do modelo de regressão linear múltipla da demanda de carne de frango com o auxílio do software Eviews 3.0 e a partir de formulários aplicados na cidade de Belém do Pará. Para estimação do modelo, escolheram-se algumas variáveis e verificaram-se quais foram aceitas para o modelo final. Foram feitos os testes necessários referentes ao modelo de regressão múltipla e analisaram-se os resultados obtidos a partir do software Eviews 3.0.
Palavras-chave: Modelagem Matemática, Oferta e Demanda, Estatística Aplicada.
Abstract
In this study, it was determined the estimation of a multiple linear regression model for the demand of chicken meat with the aid of the software Eviews 3.0 and from forms applied in the city of Belém. To estimate the model, it were chosen some variables and found which have been accepted for the final model. It were done the necessary tests for the multiple regression model and analyzed the results obtained from the software Eviews 3.0.
Keywords: Mathematical Modeling, Supply and Demand, Applied Statistics.
Para ver el artículo completo en formato pdf pulse aquí
Para citar este artículo puede utilizar el siguiente formato:
de Souza Ribeiro, de Amorim, Sabathé Vera, da Silva Tahara y Amanajás Pena: "Análise econométrica da demanda de carne de frango a partir do EVIEWS 3.0", en Observatorio de la Economía Latinoamericana, Número 169, 2012. Texto completo en http://www.eumed.net/cursecon/ecolat/br/
1. INTRODUÇÃO
O consumo de frango sofreu grandes altos e baixos ao longo da história. Após a Segunda Guerra Mundial, seu consumo se popularizou em grande parte devido à criação industrial dos animais. Até pouco tempo atrás, comer frango não era barato, entretanto, dada a grande demanda por esta carne, as aves alimentadas com grão deram lugar às criadas de forma intensiva. Assim, seu preço diminuiu de forma considerável, até o ponto de ser presentemente uma das carnes mais econômicas.
O desenvolvimento da avicultura brasileira veio a partir de um sistema de produção integrada, no Estado de Santa Catarina. Com isso, as relações entre agroindústrias e produtores se aprofundaram com contratos de participação, o que favoreceu as condições de produção e comercialização do frango (SANTANA et al., 1995).
Em 2011, foram produzidas cerca de 13 milhões de toneladas de carne de frango no Brasil, tendo um consumo per capita no país de 47,4 quilos/ano, sendo o sétimo maior consumidor de carne de frango do mundo. Portanto, visto que esse mercado é bastante representativo no setor de alimentos, decidiu-se fazer a definição de um método de regressão múltipla apropriado para relacionar o preço do frango e outras variáveis, resultando no presente artigo.
Em termos gerais visa-se analisar estatística e teoricamente os resultados do modelo de regressão múltipla especificado para a demanda de carne de frango que será estimado através do software Eviews 3.0
Mais especificamente pretende-se especificar e estimar o modelo de regressão múltipla mais adequado à série de dados relacionadas com a demanda da carne de frango, além de analisar os resultados para identificar a melhor adequação da equação sem violar as hipóteses do método de estimação e testar o modelo segundo as necessidades do modelo de regressão múltipla.
2. METODOLOGIA DA ANÁLISE ECONOMÉTRICA
2.1 COLETA DE DADOS
Para que o desenvolvimento do trabalho fosse realizado era necessária a captação de dados referente à renda familiar, número de pessoas na família (total e que contribuem para a renda familiar), quantidade adquirida de determinado itens durante as compras nos supermercados, bem como os seus preços. Os dados para estimação foram obtidos a partir da aplicação de 366 formulários aplicados no município de Belém do Pará. Os dados foram exportados para o Eviews para possibilitar a resolução do modelo.
Após a captação dos dados, os mesmos foram tratados e foi escolhido apenas um dos itens para realizar o estudo de demanda da carne de frango.
Utilizando o software Eviews 3.0, programa que auxilia nas regressões e previsões e desenvolve relações estatísticas, estimou-se o modelo de previsão de demanda do item em questão.
Foram escolhidas 16 variáveis para a estimação do modelo, que serão especificadas no modelo teórico, fez-se, então, uma primeira análise de regressão e nela foi constatado que apenas três das variáveis independentes entrariam no modelo, devido ao fato de que as demais encontravam-se fora do nível de significância de 10%. Sendo assim as variáveis restantes foram aplicadas a uma análise de regressão múltipla para obter-se a equação.
2.2 MODELO TEÓRICO
Segundo Santana (2005, p.18) “demanda é a quantidade dos bens ou serviços que os consumidores desejam e podem comprar, aos vários preços de mercado, em dado período de tempo, ceterisparibus”. Logo, as variáveis que influenciam a demanda ficam constantes e unicamente o preço varia. Na lei da demanda, a quantidade demandada apresenta relação inversa com o preço. A procura individual por um produto também é influenciada pelos desejos e necessidades das pessoas, renda do consumidor, produtos complementares e substitutos.
2.2.1 Confirmação e descrição teórica
Nesse trabalho a demanda é referente a carne de frango. Nesse caso, foram 16 as variáveis escolhida, onde a variável independente é a quantidade consumida de frango e as variáveis independentes são o preço do frango, o preço do arroz, o preço da farinha, o preço do macarrão, o preço do feijão, o preço do óleo, o preço da carne bovina, o preçoda carne suína, o preço do peixe, o preço do ovo, o preço da sardinha, o preço da carne em conserva, a despesa, a renda e a quantidade de pessoas em cada família.
De acordo com este princípio elementar da teoria econômica, teríamos o seguinte modelo teórico:
![]()
Onde as variáveis:
Qcf = Quantidade demandada de frango
(az) = preço do arroz
(far) = preço da farinha
(mac) = preço do macarrão
(fj) = preço do feijão
(ol) = preço do óleo
(cb) = preço da carne bovina
(cs) = preço da carne suína
(pf) = preço do frango
(px) = preço do peixe
(ov) = preço do ovo
(sd) = preço da sardinha
(cc) = preço da carne bovina
(dsp) = despesa
(rend) = renda
(qtdp) = quantidade de pessoas na família
2.3 MODELO MATEMÁTICO
Para uma representação simplificada da realidade, o modelo matemático utilizado foi o seguinte:
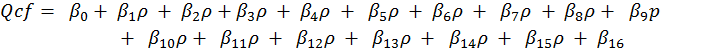
Em que:
Q é a quantidade demandada de frango;
![]() é intercepto da equação;
é intercepto da equação;
![]() representaas inclinações da equação.
representaas inclinações da equação.
2.4 MODELO ECONOMÉTRICO
Definido o modelo matemático, o próximo passo é tornar esse modelo um modelo estatístico, nesse caso, o modelo estatístico é um modelo de regressão linear múltiplo, uma vez que é um modelo especificado com mais de uma variável independente. Segundo Santana (2003, p.130) “o modelo geral de regressão linear múltipla (RLM) é uma técnica econométrica que pode ser utilizada para analisar a relação entre uma variável dependente e duas ou mais variáveis independentes”. Vale ressaltar a importância do uso do RML, uma vez que são poucas as variáveis dependentes que podem ser explicadas apenas por uma variável dependente. Com o objetivo de identificar as variáveis mais significativas do modelo, fez-se, primeiramente, a análise de regressão no software Eviews, para visualizar as variáveis que, realmente, entrarão no modelo com um nível de significância de 10%.
Tendo as variáveis escolhidas para a primeira estimação no Eviews, utilizou-se o modelo:
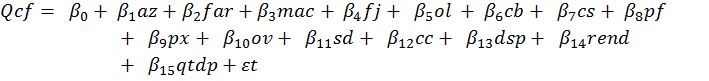
Para validação, o nível de significãncia exigido foi de 10%, será observado o valor-p das variáveis para validar o modelo estimado.
Observa-se que ao nível de 10% de significância, o modelo aceitou apenas 3 variáveis independentes, sendo elas o preço do ovo, quantidade de pessoas e a despesa. Obteve-se um valor do R² de 0.164389, significando que o modelo é capaz de explicar 16,4389% da variação na variável dependente. O coeficiente de determinação ajustado para graus de liberdade (Adjusted R-squared) teve valor de 0.128268, o que indica que 12,8268% das variações na quantidade demandada de frango são explicadas pelas variações simultâneas das variáveis independentes estabelecidas.
A grande importância de plotar o histograma é para verificar a normalidade da série, obteve-se então, o resultado do da probabilidade teste do Jarque-Bera, esse teste vai avaliar a hipótese de que determinada variável tem distribuição normal com média e variância especificada, contra a hipótese alternativa de que essa variável não tenha distribuição normal. Observa-se que a série possui uma assimetria, com um Skewness (coeficiente de simetria) de -0.254649, o índice de kurtosis (coeficiente de achatamento) e o valor obtido de para a probabilidade de Jarque-Bera foi maior que 5%, não sendo possível rejeitar-se a hipótese de distribuição normal.
Agora far-se-á a análise retirando as variáveis que não foram aceitas pelo modelo a um nível de 10%, restando apenas as variáveis aceitas: quantidade consumida de frango, preço do ovo, despesa e quantidade de pessoas.
Com as variáveis selecionadas e para a estimação no Eviews, utilizou-se o seguinte modelo:
![]()
2.5 APRESENTAÇÃO DOS DADOS ESTATÍSTICOS
A estimação segue um padrão com base no modelo definido acima a partir do software Eviews 3.0, os dados para estimação foram obtidos a partir da aplicação de 366 formulários aplicados no município de Belém do Pará. Os dados foram exportados para o Eviews para possibilitar a resolução do modelo. Ressalta-se que para melhor adequação do modelo logaritmou-se os valores utilizados.
2.6 MODELO ESTIMADO E INTERPRETAÇÃO ESTATÍSTICA
Os resultados gerados pela estimação do modelo de regressão múltipla no Eviews 3.0 para a equação a quantidade demandada de frango, levando em conta o modelo econométrico definido acima, encontram-se abaixo de acordo com formatação gerada pelo própio Eviews, que utilizou o método dos mínimos quadrados ordinários, utilizando os dados dos 366 formulários, onde temos que as observações excluídas foram 3. A partir do quadro 2 será possível estimar a equação do modelo e analisar os diversos resultados gerados pelo software.
Com isso, a partir dos coeficientes obtidos pelo software é possível definir a equação como:
![]()
Percebe-se agora que todas as variáveis foram aceitas a um nível de 10%. Obteve-se um valor de 0.119592 do R², mostrando que o modelo é capaz de explicar 11,9592% da variação na variável dependente. Tem-se também um valor do R² ajustado de 0.112235, significando que 11,2235% das variações na quantidade demandada de frango são explicadas pelas variações simultâneas das variáveis independentes estabelecidas.
Observa-se que a séria ainda continua com uma assimetria, onde coeficiente de assimetria é igual a -0.278071 e o valor de kurtosis é de 2.977185. Novamente não é possível rejeitar a hipótese de que o modelo segue a distribuição normal a um nível de 5%, uma vez que o valor da probabilidade de Jarque-Bera é maior que 5% e é possível perceber uma distribuição próxima da normal pela visualização do histograma.
2.7 VALIDAÇÃO DO MODELO
Como já foi mostrado, agora é possível afirmar que todas as variáveis são significativas estatisticamente ao nível de 10%, podendo-se, então interpretar teoricamente os dados utilizados.
Para validar o modelo foi utilizada a fórmula (100 x Valor-P) £ 10%, podendo-se aceitar as hipóteses alternativas de que as variáveis exercem influência na quantidade demandada de carne de frango.
Como outra forma de validar o modelo, utilizou o teste do tcrítico e as hipóteses teóricas estabelecidas foram testadas pelo seu correspondente valor crítico da distribuição t.
A partir do gráfico percebe-se que os resultados foram significativos, uma vez que todos os valores de t segundo o quadro 2 estão na área da hipótese alternativa, sendo possível aceitar as hipóteses alternativas. Logo, os valores das variáveis influenciam na quantidade demandada de carne de frango.
2.8 TESTE DE VALIDAÇÃO DAS HIPÓTESES
2.8.1 Teste de autocorrelação
A autocorrelação ou correlação serial é um importante problema na econometria e ocorre quando os erros nos resíduos do modelo de regressão linear estão relacionados. A presença da autocorrelação diminui a eficiência das estimativas dos parâmetros do modelo, além de que enviesa o desvio-padrão e faz com que a estatística t e R² não sejam significativas e reais. Para verificar a presença ou não de correlação, utilizou-se primeiramente o teste Durbin-Watson, que leva em conta os valores tabulados dl, que é o limite inferior, e du, que se constitui no limite superior. Para se fazer a análise, faz-se a comparação do valor encontrado para Durbin-Watson com os valores tabulados dos limites especificados anteriormente.
A partir do quadro 2, obteve-se um valor de Durbin-Watson de 1.682739, logo há presença de autocorrelação positiva, assim, para o modelo de regressão linear múltipla da demanda de carne de frango tem-se o resultado de autocorrelação positiva, ou seja, dl> d > 0, significando que os parâmetros e as estatísticas não podem ser interpretados normalmente, as fórmulas dos desvios-padrão estão viesadas e a respeito das estatísticas t e R2 as mesmas não são significativas e reais.
2.8.2 Teste de Heterocedasticidade
Teste de Park, em que se procura detectar a presença de heterocedasticidade, que é um problema que ocorre com frequência no modelo de regressão múltipla, há presença desse problema a variância do termo de erro, para o modelo de regressão não é constante para todas as observações, considerando assim que os erros são heterocedásticos, ao invés de homocedásticos, quando a variância é constante. Dado a consequência da presença de heterocedasticidade, em que o estimador do mínimo quadrados ordinários ainda é um estimador linear e não-tendencioso, os desvios-padrão são incertos, as estatísticas T e F são viesadas ou tendenciosas, logo se faz necessário fazer o teste para o modelo de regressão múltipla da demanda de carne de frango. Para realizaçãodo teste utilizou-se a significância de 10%de probabilidade.
Percebe-se que a presença de homoscedasticidade é garantida, uma vez que, por meio do teste F, o valor da probabilidade é maior que 10% (valor de significância estabelecido). Assim pode-se dizer que os estimadores e parâmetros são altamente significativos, os desvios-padrão são corretos, as estatísticas T e F não são viesados e perfeitamente reais.
2.8.3 Teste de Multicolinearidade
O problema relacionado amulticolinearidade ocorre somente no modelo de regressão múltipla, isto é, em que há a existência de mais de uma variável independente, esse problema ocorre quando as variáveis independentes ou explicativas apresentam relações lineares exatas ou aproximadamente exatas. Um modelo com a presença de multicolinearidade pode apresentar valores de R² e F elevados, ressaltando assim a relevância da realização do teste. Para realização do teste, comparam-se os valores da estatística R² com o valor do mais forte coeficiente de correlação da matriz de correlação elevado ao quadrado. Tem-se que para se aceitar a hipótese de ausência de multicolinearidade, o valor da estatística R² deve ser maior que o valor do coeficiente de correlação ao quadrado.
Como pode observar-se o maior valor da matriz de correlação é 0.3888954, elevando ao quadrado temos o valor de 0,151285214116 que é maior que o valor de 0.119592 do R². Assim, tem-se a presença de multicolinearidade. Entretanto, vale ressaltar que os parâmetros do modelo ainda são eficientes.
3.CONSIDERAÇÕES FINAIS
Logo, estimou-se, pelo software Eviews 3.0, o modelo de regressão linear múltipla da demanda de carne de frango utilizando as 15 variáveis independentes escolhidas, onde apenas 3 variáveis explicativas foram aceitas ao nível de significância de 10% .Temos que essas variáveis do modelo final, após a retirada das variáveis que não foram aceitas na primeira estimação, foram todas aceitas ao nível de significância de 10%, sendo, então, significativas. Também se obteve uma distribuição do modelo consideravelmente próxima da normal.
Observou-se que, segundo a equação do modelo estimado, que a variável preço do ovo tem uma influencia negativa para a quantidade demandada de carne de frango, isto é, quanto maior o preço do ovo, menor é a quantidade demandada de carne de frango, o que pode ter ocorrido devido a característica de bem complementardo ovo em relação a carne de frango. Também se percebe que a despesa e a quantidade de pessoas da família influenciam, segundo o modelo, positivamente na quantidade consumida de frango, ou seja, quanto maior a quantidade de pessoas e a despesa, maior é quantidade demandade frango. Além disso, caso todas as variáveis explicativas ou independentes forem 0, a quantidade demandada de carne de frango será igual a 1.
Para os coeficientes teve-se que, segundo a equação estimada do modelo, para a variação de 10% no preço do ovo, tem-se uma variação negativa de 3,2 quilogramas na quantidade demandada de carne de frango, tem-se também que para essa variação de 10% na despesa, tem-se uma variação positiva de 1 quilograma na quantidade consumida de carne de frango , e uma variação de 10% na quantidade de pessoas provoca uma variação de 3,2 quilogramas na quantidade demandada de frango.
Assim, Após os diversos testes realizados para o modelo de regressão múltipla considera-se que os resultados dos parâmetros foram eficientes, apesar dos problemas encontrados nos testes de multicolinearidade e autocorrelação, como a presença da autocorrelação positiva e da multicolinearidade.
Tem-se então o modelo de demanda da carne de frango representado pelo preço do ovo, pela quantidade de pessoas na família e pela despesa da família com alimentação.
REFERÊNCIAS:
SANTANA, A; C. Métodos Quantitativos em economia: elementos e aplicações. Belém: UFRA, 2003.
SANTANA, A; C. Elementos de economia, agronegócio e desenvolvimento local. Belém: GTZ; TUD; UFRA, 2005.
CORRAR, L.; PAULO, E.; DIAS FILHO, J. Análise Multivariada para os Cursos de Administração, Ciências Contábeis e Economia. São Paulo: Atlas, 2007.
ABRASEL. ASSOCIAÇÃO BRASILEIRA DE BARES E RESTAURANTES. Disponível em <http://www.abrasel.com.br/>. Acesso em 23, mai. 2012.
SANTANA, A. C. et al. Estudo exploratório sobre a dinâmica de produção e agroindustrialização de frango no Brasil e Região Norte. Belém: BASA; FCAP, 1995.

