Media
aritmética
(
)
La media
aritmética o simplemente media, que denotaremos por
, es el número obtenido al dividir la suma de todos los
valores de la variable entre el numero total de observaciones, y se define
por la siguiente expresión:
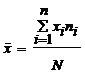
Ejemplo:
Si tenemos la siguiente distribución, se pide hallar la media aritmética, de los siguientes datos expresados en kg.
|
xi |
ni |
xi ni |
|
54 |
2 |
108 |
|
59 |
3 |
177 |
|
63 |
4 |
252 |
|
64 |
1 |
64 |
|
|
N=10 |
601 |
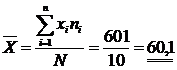kg
Si los datos están agrupados en intervalos, la expresión de la media aritmética, es la misma, pero utilizando la marca de clase (Xi).
Ejemplo:
|
(Li-1,Li] |
xi |
ni |
xi ni |
|
[30 , 40] |
35 |
3 |
105 |
|
(40 , 50] |
45 |
2 |
90 |
|
(50 , 60] |
55 |
5 |
275 |
|
|
|
10 |
470 |
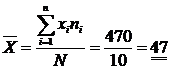
Propiedades:
1ª) Si sometemos a una variable estadística X, a un cambio de origen y escala Y = a + b X, la media aritmética de dicha variable X, varía en la misma proporción.
→
2ª) La suma de las desviaciones de los valores o datos de una variable X, respecto a su media aritmética es cero.
Ventajas e inconvenientes:
- La media aritmética viene expresada en las mismas unidades que la variable.
- En su cálculo intervienen todos los valores de la distribución.
- Es el centro de gravedad de toda la distribución, representando a todos los valores observados.
- Es única.
- Su principal inconveniente es que se ve afectada por los valores extremadamente grandes o pequeños de la distribución.
Tomado de
Ruiz Muñoz y Sánchez Sánchez
(2006) Apuntes de Estadística Edición electrónica. Texto
completo en
www.eumed.net/libros/2006/rmss/
Volver al Catálogo de Otros conceptos
