Mediana ( Me )

Dada una distribución de frecuencias con los valores ordenados de menor a mayor, llamamos mediana y la representamos por Me, al valor de la variable, que deja a su izquierda el mismo número de frecuencias que a su derecha.

·         Calculo de la mediana:

Variara según el tipo de dato:

a)   Variables discretas no agrupadas:

1º) Se calcula    y se construye la columna de las Ni ( frecuencias acumuladas )

2º) Se observa cual es la primera Ni que supera o iguala a    , distinguiéndose dos casos:

-         Si existe un valor de Xi tal que 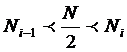 , entonces se toma como  

-         Si existe un valor i tal que 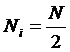   , entonces la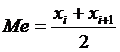

Ejemplo: Sea la distribución

lugar que ocupa             

como se produce que  ,por  lo tanto    Me = 7

El otro caso lo podemos ver en la siguiente distribución: 

Lugar que ocupa =  32/2 = 16 ==>        

Notar que en este caso se podría haber producido que hubiera una frecuencia absoluta acumulada superior a 16. En este caso se calcularía como en el ejemplo anterior.

b)   Variables agrupadas por intervalos

En este caso hay que detectar en que intervalo está el valor mediano. Dicho intervalo se denomina “ intervalo mediano ”.

Cada intervalo I_i vendrá expresado según la notación I_{i =}  ( L_i-1  , L_i ]; observando la columna de las frecuencias acumuladas, buscaremos el primer intervalo cuya Ni sea mayor o igual que , que será el intervalo modal; una vez identificado dicho intervalo, procederemos al cálculo del valor mediano, debiendo diferenciar dos casos:

1º) Si existe Ii tal que 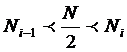 , entonces el intervalo mediano es el   ( L_i-1  , L_i ]  y la mediana es:

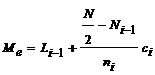
 2º) Análogamente si existe un Ii tal que 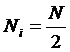  , la mediana es  

Ejemplo:

 671/2 = 335.5 ; Me  estará en el intervalo (30 - 35 ]. Por tanto realizamos el cálculo:

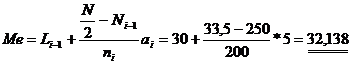
Ventajas e inconvenientes :

-         Es la medida más representativa en el caso de variables que solo admitan la escala ordinal.

-         Es fácil de calcular.

-         En la mediana solo influyen los valores centrales y es insensible a los valores extremos u “outliers ”.

-         En su determinación no intervienen todos los valores de la variable.