
Revista académica de economía
con
el Número Internacional Normalizado de
Publicaciones Seriadas ISSN
1696-8352
La Industria Automotriz en
México y el TLCAN
Un análisis de series de tiempo
Amilcar
Orlian Fernández Domínguez (CV)
afernand@uach.mx
Resumen.
El TLCAN lleva 10 años desde que se celebró y desde entonces se ha observado un crecimiento en los flujos de comercio exterior de México. La firma del tratado ha sido objeto de distintas investigaciones, muchas de ellas a nivel agregado, que tienen el propósito de evaluar los efectos de la liberalización en la economía de los miembros del tratado, esto en áreas como los salarios, los flujos de comercio en general, etc. El presente estudio analiza el impacto del tratado a un nivel más desagregado, considerando a la industria automotriz, la cual fue especialmente tratada en las negociaciones del TLCAN junto con la industria agrícola y la de textiles. Mediante técnicas de series de tiempo se encuentra que el crecimiento en el flujo de las exportaciones mexicanas de la industria automotriz es principalmente explicado por la expansión del mercado estadounidense.
Palabras clave: TLCAN, industria automotriz, series de tiempo, cointegración.
Clasificación JEL: F14
 Para citar este artículo puede utilizar el
siguiente formato:
Para citar este artículo puede utilizar el
siguiente formato:
1. Introducción.
El papel que juega la industria automotriz en la economía de México es bastante importante, pues tiene impactos en otras industrias como la del vidrio, acero y hule. Además, esta industria contribuye de manera importante a la generación de empleos[1] y a la atracción de inversión extranjera directa. Asimismo, es una de las que tiene mayor participación de producción en el sector manufacturero, como se ve en la Gráfica 1.
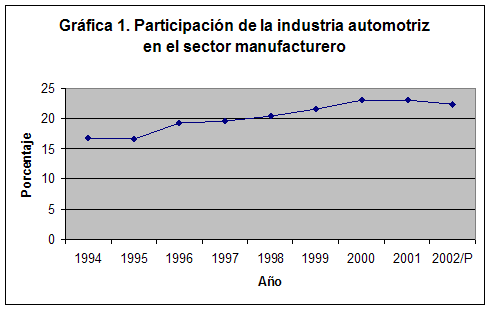
Fuente: elaboración propia con datos tomados del INEGI.
Para el año 1999, México ocupó el onceavo lugar en la producción mundial de automóviles, compitiendo con grandes productores como Italia, Bélgica y Brasil. Además, esta industria es la fuente principal de divisas dentro del sector manufacturero[2], lo cual muestra lo importante que es esta industria para el país. La cercanía con Estados Unidos hace de México un proveedor importante de bienes terminados e intermedios para las grandes ensambladoras, pues la creciente demanda del principal mercado mundial, insatisfecha por las condiciones laborales en ese país, hace que las compañías estadounidenses recurran a México, un productor eficiente, cercano y de costos bajos.
Esta industria nació en México en la década de 1920, experimentando grandes transformaciones desde entonces, y siendo durante las últimas 4 décadas una de las más dinámicas en la economía mexicana. En México no se produjeron automóviles hasta 1962, cuando un decreto automotriz obligó a las productoras a aumentar el porcentaje de componentes de origen nacional. En México se establecieron los siguientes decretos y regulaciones: Decreto Automotriz de 1962 (contenido local de 60% y había un límite máximo de producción), Regulación de 1969 y Decreto Automotriz de 1972 (fomento a la exportación, modificación a los límites de producción fijados en 1962), Decreto Automotriz de 1977 (las exportaciones son requisito para producir en México), Decreto Automotriz de 1983 (límites de producción por productora), y el Decreto Automotriz de 1989 (contenido local de 36%; busca la apertura comercial).
En la década de 1970 se dio una racha de prosperidad en la industria; el valor de producción creció a una tasa anual promedio de 10.3% entre 1975-1981. Sin embargo, la crisis de 1982 afectó a la industria, causando el cierre de varias plantas. Esto propició que el gobierno considerara nuevas medidas para mejorar las condiciones desfavorables que enfrentaba la industria[3]. De esta manera, en 1983 se emitió un decreto que limitó el número de marcas y modelos por productor, aumentó el número de partes y componentes de origen nacional y buscó fomentar las exportaciones.
Finalmente, buscando consolidar el patrón exportador de la industria y buscando una mejor especialización para competir a nivel internacional, se promulgó el último Decreto Automotriz de 1989, el Decreto para el Fomento y Modernización de la Industria Automotriz, el cual entró en vigor en noviembre de 1990. Después de entrado en vigor este decreto se experimentó un déficit en la balanza comercial de la industria causado principalmente por su dependencia en materiales de ensamble importados[4]. La industria automotriz a principios de la década de los noventa fue el resultado de la serie de decretos descritos anteriormente, así como de las condiciones macroeconómicas que tuvo el país y la competencia internacional intensa en el mercado[5].
2. El TLCAN y la industria automotriz.
En 1992, concluyeron las negociaciones del Tratado de Libre Comercio de América del Norte, el TLCAN o NAFTA por sus siglas en inglés. El interés por procurar el establecimiento de condiciones favorables para las industrias nacionales, y el monto millonario que involucraba dicho mercado, hizo de la industria automotriz una de las más discutidas en las negociaciones; entre las discusiones se tocó el calendario de disolución del Decreto Automotriz[6], pero más conflictivo aún fue el establecimiento de reglas de origen convenientes a las partes[7].
En el marco del TLCAN, se abrió el mercado mexicano a la competencia norteamericana en un periodo de transición de 10 años. Por su parte, los Estados Unidos eliminaron los aranceles sobre automóviles mexicanos (que eran bajos: 2.5%) y redujeron al 10% los aranceles sobre vehículos ligeros (eliminándose por completo en un periodo de transición de 5 años); los aranceles sobre autobuses, camiones y tractores (25%) serían eliminados en un periodo de transición de 10 años.
Sin embargo, antes de entrado en vigor el tratado, la industria automotriz ya mostraba cierta integración entre los países miembros. Desde la década de 1960, Estados Unidos y Canadá comenzaron el proceso de integración mediante el Auto Pact[8]; y en el caso de México, el proceso de integración comenzó a partir de la década de 1980. Es así como el TLCAN se volvió el instrumento que institucionalizó la integración de la industria entre los tres países.
En 1964 existían en México 7 productores en la industria, y de 1989 al año 2001 el número de plantas automotrices aumento de 13 a 30. Entre los antiguos productores que han permanecido en el país están los 3 Grandes, Ford, Daimler-Chrysler y General Motors, así como Volkswagen y Nissan. Entre las empresas nuevas se encuentran Bavarian Motor Work, con una planta en Toluca desde 1995; Mercedes Benz, establecida en 1994 y que ahora cuenta con 3 plantas en el país; Renault reingresó al mercado mexicano mediante una fusión con Nissan (en cuyas plantas realizaba operaciones de ensamblado), y en el año de 2002 inauguró su primera planta en Veracruz; Honda, con una planta en Jalisco desde 1995; y la coreana Hyundai, estableciendo un parque industrial para el año de 2001.
El número creciente de productoras establecidas en México después de entrado en vigor el TLCAN indica que se trata de una estrategia de posicionamiento de dichas empresas para cumplir con los requisitos de contenido regional del TLCAN, así como defensa de algunas contra las grandes competidoras coreanas y japonesas. Respecto a esto, la proporción de vehículos exportados a vehículos vendidos en el mercado interno se incrementó de 46.4% en 1991 a 68.8% en 1998 a pesar de que las ventas internas tuvieron un crecimiento de 40% en el mismo periodo.
En la Gráfica 2 se puede advertir que ha existido un crecimiento considerable en las exportaciones de la industria automotriz desde que entró en vigor el TLCAN; entonces, lo que se quiere probar es si éste es debido a los beneficios del tratado, cambios en las políticas económicas, y/o por el crecimiento de la economía de los Estados Unidos. En específico, se intenta probar los efectos del TLCAN en el crecimiento de las exportaciones mexicanas de la industria automotriz.
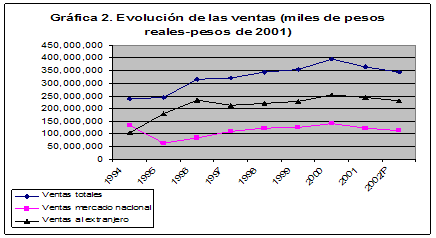
Fuente: elaboración propia con datos del INEGI.
3. Análisis econométrico.
Para encontrar la evolución que ha tenido la industria automotriz en los últimos años, así como comprobar si el TLCAN ha tenido un impacto importante en esta industria, se seguirá la metodología de Daniel Garcés (2001) en la que aplica técnicas de series de tiempo[9].Modelo base.
En febrero de 2001 Daniel Garcés Díaz publicó un trabajo donde investiga la posible relación entre el TLCAN y el crecimiento de las exportaciones mexicanas mediante técnicas de series de tiempo. Garcés utiliza una función de demanda donde las exportaciones mexicanas están en función del tipo de cambio real y la demanda de Estados Unidos:
XMex = F(Y,e)
Para el estudio econométrico, el autor utiliza un modelo log-log, quedando la demanda de exportaciones explicada de la siguiente manera:
lXt = α0 + α1 lYt + α2 let + ut
Dado el modelo anterior y la naturaleza de los datos, el autor realizó su investigación en dos etapas: primeramente estimó la relación de largo plazo entre las variables mediante técnicas de cointegración (metodología de Johansen), y posteriormente aplicó el mecanismo de corrección de errores para estimar las relaciones de corto plazo y largo plazo. Para esto, Garcés utilizó datos mensuales desde 1980 hasta 2000, donde las exportaciones mexicanas se analizaron a nivel agregado y a nivel desagregado (maquila, exportaciones petroleras, y el resto), la demanda se aproximó mediante el índice del volumen de producción industrial de Estados Unidos, y usó el tipo de cambio real peso-dólar.
Respecto a los resultados encontrados en su investigación, Garcés no encontró evidencia de que el TLCAN haya contribuido al crecimiento de las exportaciones analizando el periodo 1990-2000, sino que dicho crecimiento se debió en mayor parte a la expansión en la economía estadounidense[10].
Metodología.
De esta manera, en el presente estudio se tomará como base la metodología seguida por Garcés, quedando de la siguiente manera: primeramente se realizarán pruebas de raíz unitaria para verificar si las variables son estacionarias o no. Posteriormente se llevará a cabo la prueba de cointegración de las variables, así como el análisis sobre la posible existencia de un cambio estructural en la relación de largo plazo. Por último, en base a los resultados se analizará la relación de las variables en el contexto del modelo de corrección de errores.
Datos.
El periodo que se cubrirá en el análisis abarcará desde enero de 1991 hasta junio de 2001,[11] utilizando datos mensuales para las variables mencionadas anteriormente, es decir, exportaciones del sector automotriz, tipo de cambio real y el índice del volumen de producción industrial de Estados Unidos. Dado que las exportaciones de México hacia Estados Unidos son las importaciones de Estados Unidos desde México, se ocuparán datos desagregados de importaciones reales[12] conforme al Sistema Armonizado a niveles de partida (4 dígitos) que incluyen aquellos valores de las partidas 8701 a la 8703[13]; estos datos son tomados del World Trade Atlas. Además, se utilizará el tipo de cambio real peso-dólar construido a partir de los respectivos índices de precios (esto es, CPI tanto de Estados Unidos como de México con base 2002) tomado del Banco de México; y se utilizará el índice de producción industrial de Estados Unidos con base 2002=100 tomado del Bureau of Labor Statistics (US Department of Labor).De esta manera, antes de iniciar el análisis econométrico, es conveniente hacer un análisis gráfico de las variables. Respecto al tipo de cambio real, puede observarse en la Gráfica 3.1 el brinco en la tendencia por la devaluación en 1995. A partir de entonces, se observa una valuación paulatina de la moneda, es decir, el peso ha ganado terreno con respecto al dólar, marcado por la pendiente negativa.
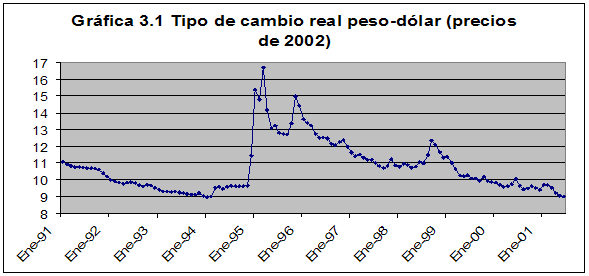
Fuente: elaboración propia con datos de Banxico y Bureau of Labor Statistics.
Por su parte, en la Gráfica 3.2 se observa que el valor de las exportaciones reales de automóviles desde México a los Estados Unidos ha tenido un crecimiento desde el comienzo del periodo de estudio hasta finales del año 2000; desde entonces las exportaciones se estancaron. Es importante hacer notar que, como se verá posteriormente, existe una relación inversa entre el tipo de cambio real y el valor de exportaciones reales, es decir, aunque el peso se va haciendo más caro con respecto al dólar, las exportaciones de automóviles siguen creciendo.
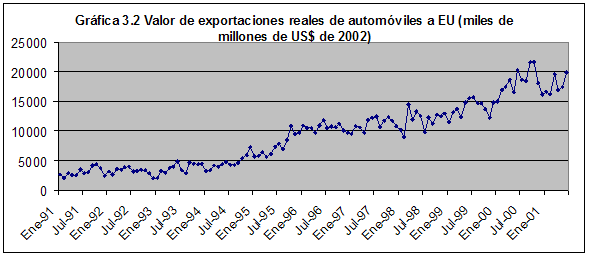
Fuente: elaboración propia con datos del World Trade Atlas y Bureau of Labor Statistics.
Por último, en la Gráfica 3.3 se observa que el índice del volumen de producción industrial de los Estados Unidos ha tenido una tendencia positiva durante todo el periodo de análisis. A partir de octubre del año 2001 el índice dejó de tener la tendencia positiva que había tenido en los últimos años.
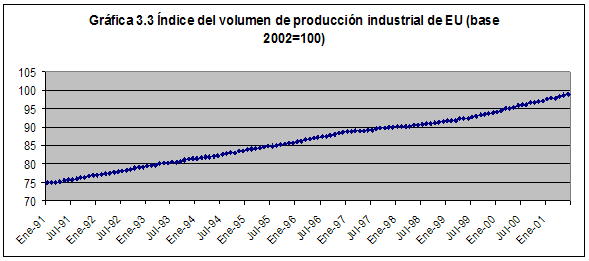
Fuente: Bureau of Labor Statistics.
De esta manera, viendo el comportamiento de las variables durante el periodo de análisis (sabiendo que no existen comportamientos extraños o si hay datos outliers en la muestra) se continuará con el análisis econométrico.
Pruebas de raíz unitaria.
Como se mencionó anteriormente, la relación que se pretende analizar se puede expresar de la siguiente manera:
lXt = α0 + α1 lYt + α2 let + ut
donde se puede realizar una prueba Chow para analizar el posible cambio estructural causado por el TLCAN. Sin embargo, los coeficientes obtenidos mediante OLS pueden ser objeto de una regresión espuria dada la naturaleza de las variables (son series de tiempo)[14], es decir, pueden ser no estacionarias. Es por esto que se deben hacer pruebas de raíz unitaria. Además, Hansen (2001) menciona que la prueba de Chow está limitada a que la fecha de quiebre debe ser conocida, pues los resultados de la prueba pueden ser muy sensibles ante elecciones arbitrarias sobre el punto de quiebre: si se elige arbitrariamente un punto cualquiera puede ser no informativo dado que se pierde el punto de quiebre verdadero; si se elige un punto de quiebre en base a alguna característica de los datos los resultados pueden ser engañosos. Por lo tanto, sugiere Hansen (2001) emplear métodos más adecuados (tratar la fecha como desconocida)[15]. Entonces, para verificar que las variables sean integradas de orden uno, es decir, no estacionarias, se utilizará el método de Dickey-Fuller Aumentada (ADF) para raíces unitarias. La Tabla 3.1 presenta los resultados obtenidos mediante la aplicación de la prueba Dickey-Fuller Aumentada para los niveles en logaritmo de las variables que se mencionan. El número de rezagos se muestra en base al criterio de Schwartz, Akaike y Hannan-Quin[16].
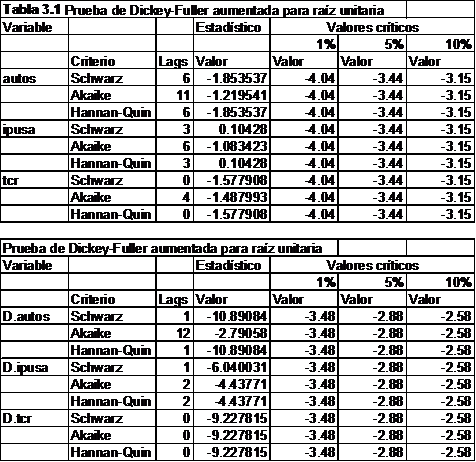
La primera parte de la Tabla 3.1 muestra las pruebas de raíz unitaria a los niveles de las variables (con tendencia). En todos los casos se puede observar que no se puede rechazar la hipótesis nula de raíz unitaria, lo cual confirma que las variables son no estacionarias. Ahora, al aplicarles la prueba a las primeras diferencias de las variables, se observa que únicamente en el caso del criterio de Akaike no se puede rechazar la hipótesis de raíz unitaria en la primera diferencia de las importaciones de automóviles a niveles del 5%, sin embargo, a niveles de 10% y bajo los otros dos criterios se rechaza la hipótesis. Por lo tanto, se considerará a las variables como integradas de orden uno, I(1) en niveles, y I(0) en primeras diferencias.
Cointegración y cambio estructural.
Dados los resultados anteriores, es posible realizar OLS para la siguiente ecuación:
∆lXt = β0 + β1 ∆lYt + β2 ∆let + εt
Sin embargo, se pierde información respecto a la relación de largo plazo que existe entre las variables. En este sentido, es necesario analizar si las variables se encuentran cointegradas, es decir, si tienen una relación a largo plazo.
Como mencionan Villanueva y McCown (2005), se puede pensar que exista una relación de largo plazo estable entre dos variables integradas de orden uno (no estables) durante un periodo de tiempo siempre que no haya un cambio estructural en los parámetros[17], es decir, considerando las variables X y Y integradas de orden uno, se tiene el siguiente modelo de cointegración sin cambios estructurales:Yt= a0 + a1Xt + ut
donde, bajo cointegración, el error u es integrado de orden cero I(0) y a0 es una constante.
Si embargo, Gregory y Hansen (1996) sugieren la posibilidad de que el vector de cointegración cambie en un punto en el tiempo. Entonces en la relación de largo plazo se puede incorporar una variable dummy igual a 1 a partir del punto en el tiempo en que se da el cambio estructural manteniendo la cointegración de las variables, quedando el modelo de cointegración:
Yt= a0 + a1Dt + a2Xt + a3DtXt + ut
donde a0 denota el intercepto de cointegración y a2 denota la pendiente de cointegración antes del cambio estructural; y (a0+a1) denota el intercepto de cointegración y (a2+a3) denota la pendiente de cointegración después del cambio estructural.
Considerando lo anterior, dado que las variables de importaciones de automóviles, tipo de cambio real y producción industrial son integradas de orden uno, se esperaría que, en caso de no existir un cambio estructural (causado por el TLCAN u otro evento), el modelo de cointegración Yt= a0 + a1Xt + ut estará bien especificado y por lo tanto el error ut será I(0), dado que la hipótesis nula es “no cointegración”[18]. Si el modelo de cointegración sin cambio estructural rechaza la hipótesis nula (ut sería I(0)), entonces, mencionan Villanueva y McCown, “la simple hipótesis de cointegración sin cambios estructurales debería ser considerada como validada por los datos aun si el modelo con cambios estructurales también rechaza la hipótesis nula”. Por otra parte, en el caso en que el modelo de cointegración sin cambios estructurales rechace la hipótesis de cointegración, entonces los rechazos de la hipótesis nula por el modelo alternativo (el que incluye la dummy) se vuelven relevantes e indicativos de cambios estructurales en determinado punto en el tiempo.Por consiguiente, primeramente se considerará el modelo de cointegración sin cambios estructurales. Realizando la prueba de raíz unitaria al residuo ut en el modelo de cointegración
lmautt= a0 + a1lipusat + a2ltcrt + ut
se rechaza la hipótesis nula, como se muestra en la Tabla 3.2:

lmautt= c + 4.39lipusat + .79ltcrt
(.1127) (.1222)
lo cual indica que si la economía estadounidense crece en 1%, se espera que las exportaciones de automóviles aumenten en 4% aproximadamente. Asimismo, si el tipo de cambio real aumenta en 1% (el peso se devalúa con respecto al dólar), se espera que las exportaciones aumenten un .79%.
Aplicando la prueba de Johansen para cointegración se obtienen resultados similares:
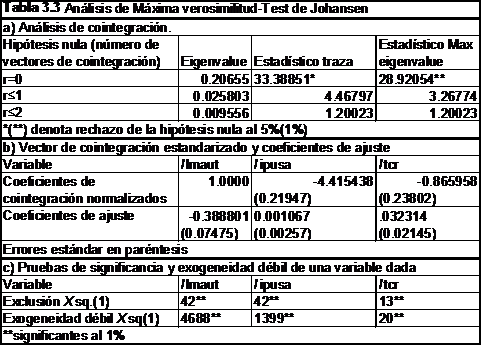
En la sección a) de la Tabla 3.3 se muestran los eigenvalues y estadísticos de traza y max-eigenvalue para la secuencia de hipótesis nulas de cero, al menos uno y al menos dos vectores de cointegración[21]. Ambos estadísticos rechazan la hipótesis nula de que hay cero vectores de cointegración, pero no rechazan la hipótesis de que hay un vector de cointegración, por lo que se concluye que la relación de largo plazo entre las variables está definida por un solo vector de cointegración. La sección b) muestra los coeficientes de cointegración normalizados los cuales presentan coeficientes similares a los obtenidos anteriormente. Los coeficientes de la función de demanda de largo plazo obtenidos son (errores estándar en paréntesis):
lmautt= c + 4.41lipusat + .86ltcrt
(0.2194) (.2380)
Por último, en la sección c) se muestran las pruebas de exclusión (likelihood ratio test) y el de exogeneidad débil (Wald test) para ver si las variables entran en el vector de cointegración. Dado que en todos los casos las variables son significativas, se concluye que no pueden ser omitidas del vector de cointegración.
Ahora, suponiendo que se es un tanto escéptico respecto a los resultados encontrados hasta ahora y que sí hubiera un cambio estructural, y para comprobar si dichos resultados son robustos, entonces se puede seguir la metodología explicada por Villanueva y McCown (2005)[22] para encontrar el punto en el tiempo en que surge el cambio estructural: se considera el modeloYt= a0 + a1Dt + a2Xt + a3DtXt + ut
y se supone que el cambio estructural se da en un punto intermedio de la muestra comprendido en los percentiles (.15 , .85)[23]. Entonces primeramente se corre el modelo donde D=0 desde la observación 1 a la que corresponda al percentil .15, digamos n, y D=1 a partir de la siguiente observación n+1. Luego se corre el modelo donde D=0 desde la observación 1 a la n+1 y D=1 a partir de n+2; este proceso se repite hasta que se alcanza la observación comprendida en el percentil .85. Se rescatan los errores de cada regresión y se les aplica la prueba de raíz unitaria ADF, generando de esta manera una serie de estadísticos ADF*; entonces, explican los autores, el punto de quiebre es aquel dado por el valor mínimo de estos estadísticos. Aplicando esta metodología[24], en nuestra muestra el valor mínimo se da en la observación 56, es decir, el mes de agosto del año 1995:
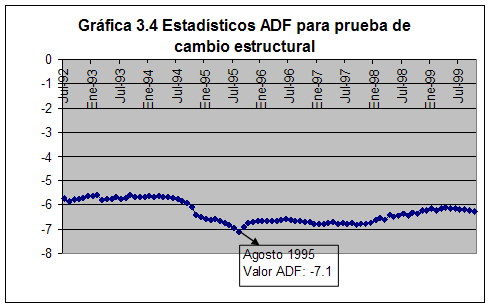
Por lo tanto, dado este punto de quiebre el modelo de cointegración quedaría explicado de la siguiente manera:
lmautt= a0 + a1Dt + a2lipusat + a3Dtlipusat + a4ltcrt + a5Dtltcrt+ ut
donde D=1 a partir de agosto de 1995.
Los coeficientes de la función de demanda de largo plazo obtenidos considerando un cambio estructural en agosto de 1995 son (errores estándar en paréntesis):
lmautt= a0 + 15.17Dt + 4.52lipusat – 2.81Dtlipusat + .36ltcrt - .97Dtltcrt
(3.7767) (.43633) (.69911) (.16469) (.42135)
indicando que antes del punto de quiebre, si la economía estadounidense crecía en 1%, las exportaciones de automóviles aumentaban más de 4% (resultado similar al obtenido anteriormente), si el tipo de cambio real aumentaba 1%, las exportaciones de automóviles crecían en .36%; pero después del punto de quiebre, si la economía estadounidense crecía 1%, las exportaciones de automóviles aumentaban en menos de 2%, es decir, la elasticidad de la demanda disminuyó. Por su parte, el coeficiente del tipo de cambio real posterior al quiebre (Dtltcrt) no es estadísticamente significativo.
Modelo de corrección de errores.
Para la elaboración de los modelos de corrección de errores, se tomaron los rezagos indicados en las pruebas de Breusch-Pagan y Portmanteau realizadas anteriormente para el establecimiento del número de rezagos que se debían incluir en el VAR de la prueba de Johansen[25]. Así, primeramente considerando estabilidad en la relación de largo plazo se tienen los siguientes modelos:

Como se puede observar en la Tabla 3.4, los coeficientes de velocidad de ajuste, esto es, los del vector de cointegración, son negativos y estadísticamente significativos, lo cual reafirma la hipótesis de que existe una relación de largo plazo. En todos los casos la velocidad de ajuste es alta, indicando que no se requiere mucho tiempo para regresar al equilibrio en caso de que haya desajustes en la relación de largo plazo.
Siguiendo a Garcés[26], se incluyó en el modelo una variable dummy igual a 1 a partir de los años 1993 (para ver si hubo una anticipación del TLCAN), 1994 (entrada en vigor del tratado), y para enero y agosto de 1995 (por si hubo un efecto post-TLCAN) resultando ser no significante en todos los casos, es decir, no se encuentra evidencia para confirmar la hipótesis de que hay un cambio estructural.Ahora, considerando el modelo de cointegración con cambio estructural a partir de agosto de 1995, se tienen los siguientes modelos de corrección de errores:

Al igual que en el caso del modelo de cointegración sin cambios estructurales, los coeficientes de velocidad de ajuste son negativos y estadísticamente significativos. Ahora, en estos modelos la velocidad de ajuste es mayor; se requiere poco tiempo para regresar al equilibrio en caso de que haya desajustes en la relación de largo plazo. Asimismo, como en el caso anterior, siguiendo a Garcés se incluyó una variable dummy igual a 1 a partir de las mismas fechas (enero de 1993, 1994 y 1995, y agosto de 1995) y no se pudo rechazar la hipótesis nula de que no hay un cambio estructural causado por el TLCAN antes y después de entrado en vigor el tratado.
Conclusiones.
En el presente trabajo se analizó la evolución de exportaciones de la industria automotriz hacia los Estados Unidos mediante técnicas de series de tiempo. El estudio abarcó el periodo de enero de 1991 a junio de 2001 utilizando datos mensuales de variables no estacionarias, integradas de orden uno.
Se encontró que para el periodo de estudio la relación entre las exportaciones reales mexicanas de vehículos automotores como función del índice del volumen de producción industrial de Estados Unidos y del tipo de cambio real peso-dólar es estable (descartando la posibilidad de quiebres estructurales), es decir, existe una relación de largo plazo entre estas variables.
Se encontró que existe un vector de cointegración entre las variables mencionadas anteriormente, obteniéndose coeficientes con el signo esperado. Al realizar los modelos de corrección de errores, se observa una velocidad de ajuste alta, indicando que esta industria no permite desequilibrios prolongados en la relación de largo plazo, sino que se ajusta de manera rápida[27]. Ninguna de las variables en dicho modelo fue significativa salvo el tipo de cambio real rezagado, el cual entra con signo negativo.Para comprobar si los resultados son robustos, se probó la existencia de un cambio estructural en la relación de largo plazo de las variables, dando como fecha de quiebre agosto del año 1995. Al incluir este vector de cointegración con cambio estructural en el modelo de corrección de errores se obtuvo nuevamente una velocidad de ajuste alta, y nuevamente los coeficientes de las demás variables (incluyendo el tipo de cambio real) fueron no significativos.
Por último, diversas dummies fueron introducidas en los modelos para controlar los posibles efectos del TLCAN al explicar el crecimiento de las exportaciones de la industria automotriz, siendo no significativas en todos los casos, lo que confirma que dicho crecimiento se debe en mayor medida al crecimiento de la economía estadounidense, así como la integración que se venía dando en la industria antes de entrado en vigor el tratado.
Además, es importante recordar que el TLCAN brindó beneficios preferenciales bajos a la industria automotriz mexicana, específicamente tratándose de automóviles, pues aunque el tratado eliminó por completo las tarifas arancelarias estadounidenses a la importación de automóviles producidos en México, antes de entrado en vigor el tratado los aranceles a dichos bienes eran mínimos: solamente del 2.5%.
Referencias.
Arranz, Miguel A. y Escribano, Álvaro. Cointegration testing under structural breaks: a robust extended error correction model. Oxford Bulletin of economics and statistics, 62. 2000.
Bancomext. La industria automotriz en México. Oportunidades de negocio 2004. www.bancomext.com
Bardán E, Cuitláhuac (coordinador). La industria automotriz en el TLCAN: implicaciones para México. Instituto de Investigaciones Legislativas del Senado de la República. Julio 2003.
Berry, Steven y Grillo, Vittorio. The automobile industry and the Mexico-US free trade agreement. NBER Agosto 1992.
Bureau of Labor Statistics. http://stats.bls.gov/
Carone, Giuseppe. Modeling the U.S. demand for imports through Cointegration and error correction. Journal of Policy Modeling Febrero 1996.
Cuthbertson, Keith, Hall, Stephen G. y Taylor Mark P. Advanced econometric techniques. University of Michigan Press. 1992.
Frankel, Jeffrey A. y Romer, David. Trade and Growth: an empirical investigation. NBER Marzo 1996.
Garcés-Díaz, Daniel. Was NAFTA behind the Mexican export boom (1994-2000)? Banco de México. Febrero 2001.
García-Bullet, Sérgio. NAFTA-La experiencia mexicana. Presentación para la Fundación Casimiro Montenegro Filho. Seminario: ALCA y su impacto en el Desarrollo Tecnológico Brasileño. Booz Allen Hamilton 2002. http://www.fcmf.org.br/files/PalestraAlca.html
Gregory, Allan y Hansen, Bruce. Residual-based tests for cointegration in models with regime shifts. Journal of Econometrics 70. 1996.
Hansen, Bruce E. The new econometrics of structural change: dating breaks in U.S. labor productivity. Journal of Economic Perspectives. Vol. 15, No. 4. 2001.
Hansen, H. y Johansen, S. Some tests for parameter constancy in cointegrated VAR-models. Econometrics Journal, Vol 2. 1999.
Hansen, Peter R. Structural changes in the cointegrated vector autoregressive model. Brown University working paper. Septiembre 2001.
Hanson, Gordon. What Has Happened to Wages in Mexico since NAFTA? Implications for Hemispheric Free Trade. NBER. Marzo 2003.
INEGI. Banco de información económica (BIE). www.inegi.gob.mx
Johnson, Jon R. NAFTA and the trade in automotive goods. The Fraser Institute. 1999.http://www.fraserinstitute.ca/
Krueger, Anne O. Trade creation and trade divertion under NAFTA. NBER Diciembre 1999.
Lee, Ha Yan, Ricci, Luca Antonio y Rigobon, Roberto. Once again, is openness good for growth? IMF. Julio 2004. WP/04/135.
Ramírez, José Carlos. Los efectos del TLCAN sobre el comercio y la industria de México. Pp. 181-217 en Borja Tamayo, Arturo; coordinador. Para evaluar al TLCAN. Editorial ITESM 2001.
Richards, Eric L. Law for Global Business. Irwin 1994.
Soloaga, Isidro y Winters, L. Alan. Regionalism in the Nineties: what effect on trade? WB 2001.
Tornell, Aaron, Westermann, Frank y Martinez, Lorenza. NAFTA and Mexico’s less than stellar performance. NBER Febrero 2004.
USITC. Investigation No. 332-381: the impact of the North American Free Trade Agreement on the U.S. Economy and Industries: a three-year review. USITC 1997.
USTR Report (Office of the United States Trade Representative). Study on the operation and effect of the NAFTA. USTR. http://usinfo.org/trade/nafta/chap2_2.stm.html
Valverde Loya, Miguel Ángel. Cómo Bush y Clinton lograron vender el TLCAN al Congreso de Estados Unidos, y lo que aprendimos de ello. Pp. 101-139 en Borja Tamayo, Arturo; coordinador. Para evaluar al TLCAN. Editorial ITESM 2001.
Villanueva, Miguel y McCown, James R. Structural breaks and spot-forward cointegration in fx markets. Social Science Research Network. Febrero 2005.
Womack, James P. The Mexican motor industry: strategies for the 1990’s. MIT International Motor Vehicle Program International Policy Forum. Mayo 1989, p. 19.
Wooldridge, Jeffrey M. Introductory Econometrics. A Modern Approach. Thomson South Western. 2E 2003.
World Trade Atlas. www.gtis.com
[1] Ramírez (2001) señala que para 1998 empleó a 395 mil personas.
[2] El Instituto de Investigaciones Legislativas del Senado señala que a partir de entrado en vigor el TLCAN, la industria automotriz logró ser más importante que el petróleo y el turismo como fuente de divisas.
[3] El país se enfrentaba, además del problema de la disminución de la demanda interna causada por la crisis, a la agudización en la tendencia de producción integrada globalmente, lo que provocó modificar el enfoque (hacia las exportaciones) y ubicación de la producción (centro y norte del país).
[4] En 1991 la industria tuvo un déficit de USD$1274 millones.
[5] El Decreto Automotriz tenía un esquema regulatorio más restrictivo que el Auto Pact establecido entre Canadá y los Estados Unidos, aunque los dos tenían el objetivo de mantener un nivel de valor agregado nacional en la producción de automóviles.
[6] La diferencia entre el Decreto y el TLCAN radica en los porcentajes y tiempos de desregulación.
[7] Dos de los 3 Grandes (Ford y Chrysler) estaban interesadas en un 70% de origen nacional, mientras que el otro grande General Motors apoyaba un 60%. Los mexicanos y los canadienses apoyaron la idea de un 60%. Sin embargo, al final se aprobó un 62.5% a pesar del disgusto manifiesto de algunos como Harold Poling, presidente de Ford.
[8] El nombre completo es Acuerdo Concerniente a Productos Automotrices entre el Gobierno de Canadá y el Gobierno de los Estados Unidos (Agreement Concerning Automotive Products between the Government of Canada and the Government of the United States), entró en efecto en 1966 y su objetivo era la entrada libre a los Estados Unidos bajo determinados criterios de origen de los bienes.
[9] La Comisión de Comercio Internacional de Estados Unidos llevó a cabo una investigación similar para evaluar el impacto del TLCAN en las economías de los países miembros para tres años de entrado en vigor el tratado, es decir, hasta diciembre de 1996.
[10] Otras investigaciones como la de Krueger (1999) y la de Soloaga y Winters (2001) encuentran resultados similares mediante modelos de gravedad. Krueger concluye que otros efectos, como la reducción de tarifas y la modificación del tipo de cambio, fueron más significativos que el TLCAN. Soloaga y Winters no encuentran que el TLCAN haya tenido un impacto significativo explicando el crecimiento de comercio entre los miembros.
[11] No se incluyen observaciones posteriores a esta fecha para realizar el análisis hasta el ciclo Clinton y evitar que los efectos causados por el “september 11” afecten el análisis. De esta manera, se tiene un periodo considerable (casi siete años) posterior al TLCAN, tiempo suficiente para permitir movimientos de capital y otros efectos causados por el tratado.
[12] Se deflactó en base al IPC de Estados Unidos de 2002.
[13] Estas partidas incluyen los automóviles concebidos para el transporte de personas y tractores.
[14] Hansen (2001) cita autores que han demostrado que varias series de tiempo macroeconómicas son caracterizadas por una caminata aleatoria: en vez de tener una tendencia fija a la cual la serie se revierte durante el ciclo, la tendencia se moverá a causa de shocks aleatorios, permaneciendo en la nueva tendencia hasta que llegue otro shock aleatorio.
[15] Al respecto, en el presente estudio se seguirá un método (bajo el contexto de cointegración) que considera la fecha de quiebre como desconocida, pues aunque la fecha de entrada en vigor del TLCAN es conocida (1 de enero de 1994), puede esperarse que las empresas reaccionen al establecimiento del tratado antes o después de su fecha de entrada en vigor, es decir, puede esperarse una anticipación al tratado o una dilación. Este método y los autores se comentan en la siguiente sección “Cointegración y cambio estructural”.
[16] El propósito de incluir rezagos en la prueba de Dickey-Fuller Aumentada es el de tratar el problema de correlación serial en los errores. Los criterios de Schwartz, Akaike y Hannan-Quin pretenden minimizar el número de rezagos para tratar este problema sin perder muchos grados de libertad. Villanueva y McCown (2005) citan la recomendación de usar el criterio de Akaike dada por algunos autores.
[17] Existe una basta literatura referente a los cambios estructurales en el contexto de cointegración. Hansen (2001) menciona distintos enfoques tomados por diversos autores para modelar cambios estructurales, como por ejemplo Hansen y Johansen (1999), los cuales utilizan métodos de estimación recursiva, y Gregory y Hansen (1996), los cuales desarrollaron unas pruebas de cointegración basadas en residuos. Respecto a esto, en este trabajo se sigue la metodología de Villanueva y McCown (2005), la cual es una aplicación de Gregory y Hansen (1996).
[18] Villanueva y McCown citan autores que muestran que un cambio estructural puede ser confundido por raíz unitaria en los tests. Arranz y Escribano (2000) mencionan que si un shock no es considerado, las pruebas de raíz unitaria estándares en general confundirán el cambio estructural por raíz unitaria.
[19] Además de lo que se citó anteriormente de Villanueva y McCown (2001) sobre la validación de la hipótesis de cointegración sin cambio estructural, Gregory y Hansen (1996) mencionan que si hay un cambio de régimen en el vector de cointegración, la prueba ADF no rechazará la hipótesis nula y se concluirá erróneamente que no hay relación de largo plazo. Además mencionan estos autores que si los tests ADF y ADF* (realizado posteriormente para comprobar la robustez de los resultados) rechazan la hipótesis de no cointegración, sería inapropiado concluir que hay cambio estructural, y entonces hay garantía de que no hay dicho cambio estructural. Si sólo una de las pruebas (ADF o ADF*) rechaza la hipótesis de no cointegración, entonces esto implica que hay alguna relación de largo plazo.
[20] Cuando una combinación lineal de dos variables integradas de orden uno es integrada de orden cero, es decir, dadas las variables X y Y, I(1), una regresión en niveles de X y Y no es espuria si existe una variable s que sea I(0) dado s=X-βY.
[21] La prueba de Johansen es una secuencia de tests; calcula los eigenvalues y estadísticos de traza y maxeigenvalue para un VAR definido por un sistema de variables I(1). Se aplicaron el test de Breusch-Pagan (independencia de residuos entre ecuaciones) y la de Portmanteau (residuos de ruido blanco) para definir el número de rezagos incluidos en el VAR, los cuales dieron 1 rezago.
[22] Como se menciona anteriormente, estos autores realizan una aplicación sobre la prueba de un punto de quiebre en los vectores de cointegración para una fecha desconocida. Para más información, diversas pruebas de este tipo fueron desarrolladas por Gregory y Hansen (1996).
[23] Este criterio se sigue por convención para dar un margen considerable de observaciones antes y después del punto de quiebre a la estimación. Para más ejemplos ver Gregory y Hansen (1996) y sus referencias.
[24] En la prueba ADF se incluyeron 0 rezagos conforme al criterio de Schwarz.
[25] En los paquetes estadísticos Eviews y Stata se construyen los modelos de corrección de errores a partir de este VAR.
[26] Arranz y Escribano (2000) citan algunos estudios referentes a la inclusión de dummies para capturar cambios estructurales en los modelos de corrección de errores.
[27]
Ramírez (2001) señala que las empresas relacionadas con la industria
automotriz han adaptado sus sistemas de manufactura al conocido sistema de
producción “justo a tiempo” (just in time); esto indica que los movimientos
en las operaciones comerciales de la industria dejan poco lugar a desajustes
a lo largo del tiempo.

