
Revista académica de economía
con
el Número Internacional Normalizado de
Publicaciones Seriadas ISSN
1696-8352
ANÁLISE ECONOMÉTRICA DA DEMANDA DE FARINHA DE MANDIOCA A PARTIR DO EVIEWS 3.0
Bernardo Nunez Brega
Deiglison Valente de Seixas
Leon David Serruya
Luiz Paulo Fialka Soares
Heriberto Wagner Amanajás Pena (CV)
heripena@yahoo.com.br
UEPA
Resumo
No trabalho presente foi estimado o modelo de regressão linear múltipla da demanda da farinha de mandioca, usando o software Eviews 3.0 e o levantamento de dados através de questionários em um determinado bairro da cidade de Belém do Pará. Foram feitos os testes necessários referentes ao modelo de regressão múltipla e analisaram-se os resultados obtidos a partir do software Eviews 3.0.
Palavras-chave: regressão linear, demanda, modelo estatístico, oferta e mercado.
Abstract
In the present work was estimated multiple linear regression model of the demand for cassava flour, using Eviews 3.0 software and data collection through questionnaires in a certain neighborhood of the city of Belém do Pará has been made the necessary tests for the model multiple regression and analyzed the results obtained from the software Eviews 3.0.
Keywords: linear regression and demand; statistical model, supply and market.
Para ver el artículo completo en formato pdf pulse aquí
Para citar este artículo puede utilizar el siguiente formato:
Nunez Brega, Valente de Seixas, Serruya, Fialka Soares y Amanajás Pena: "Análise econométrica da demanda de farinha de Mandioca a partir do EVIEWS 3.0", en Observatorio de la Economía Latinoamericana, Número 169, 2012. Texto completo en http://www.eumed.net/cursecon/ecolat/br/
1. INTRODUÇÃO
Um dos alimentos mais consumidos pelos brasileiros é a farinha de mandioca, seu consumo remonta aos tempos da colonização. É um alimento consumido por todas as classes sociais. Caracteriza–se em um alimento de alto valor energético, rico em amido, contém fibras e alguns minerais como potássio, cálcio, fósforo, sódio e ferro.
No Pará, é usada tanto em pratos simples, como o chibé, que é muito popular entre os menos favorecidos economicamente, quanto em pratos mais sofisticados. É o estado com a maior produção nacional, com um milhão de toneladas anuais e 300 mil hectares plantados. Na região amazônica é comumente utilizada em conjunto com outro alimento característico da região, o açaí.
Tem grande importância histórica, econômica e social na nossa região. Com uma produção fortemente artesanal, tornou-se um alimento formador de culturas e de relacionamentos sociais. Fortemente presente no imaginário indígena desde os tempos pré-colonização, sendo o principal alimento nesse período da nossa história.
Levada para África pelos colonizadores portugueses, graças a sua fácil capacidade de adaptação, rapidamente se expandiu pelo mundo. Hoje é produzida em mais de 80 países, com o Brasil ocupando o segundo lugar entre os maiores produtores.
Sua fabricação se dá a partir da mandioca puba mole, retira-se a mandioca da roça, que vai para o poço e permanece por três dias. Depois de macerada na água para fermentar, amolece-a facilitando a extração da casca. A mandioca é em seguida amassada e triturada sobre uma tábua, formando-se uma papa, depois é introduzida no tipiti, separada pela curera. Finalmente leva-se ao forno, de onde sai seca e torrada.
Apesar de constituir a forma mais ampla de aproveitamento industrial da mandioca, ela não é um produto muito valorizado, sobretudo pela falta de uniformidade. Essa heterogeneidade é devida principalmente à fabricação por pequenos produtores para seu uso, cada um deles seguindo processo próprio, além de existirem muitos tipos de farinha nas diferentes regiões do Brasil.
O objetivo deste artigo é ter o conhecimento de quanto o preço e a demanda da farinha influenciam no aumento ou diminuição da demanda de outros alimentos da cesta básica. De forma a conhecer quais são os itens complementares e substitutos da farinha.
- Captação de dados para a análise estatística
Para possibilitar o desenvolvimento deste presente estudo, fez-se necessário a realização de pesquisas de campo para a coleta de dados. Foram preenchidos 366 formulários em diversos supermercados da cidade de Belém, no estado do Pará. Após a coleta dos dados, foi feito o tratamento dos mesmos no software EVIEWS 3.0, buscando a realização de testes de regressão.
Os formulários continham os seguintes dados: Renda familiar, gasto mensal com alimentação, número de pessoas na família, quantidade consumida de 24 itens da cesta básica e seus respectivos preços.
Para a análise estatística foi escolhido um item da cesta básica para cada grupo. No caso deste, a variável escolhida foi a quantidade demandada da farinha de mandioca. A análise objetivava descobrir quais itens influenciavam na variação da demanda da farinha.
Primeiramente foram selecionados 12 itens que se relacionam com o consumo da farinha no município de Belém, mais as seguintes variáveis: despesa, preço da farinha, quantidade de farinha, quantidade de pessoas, renda, resíduos e uma constante C. Após a realização do teste, excluiu-se 14 variáveis que não se enquadravam no nível de 10% de significância estipulado pelo grupo.
Dessa forma, a análise de regressão múltipla foi feita com as seguintes variáveis: Açaí, carne bovina, carne de frango, farinha de tapioca e preço da farinha de mandioca. A partir destes gerou-se a equação geral da demanda.
- Modelo Teórico
Na economia, existe um fator preponderante que rege as transações de mercado, que é a Teoria da Oferta e da Demanda. Esta teoria mostra como funciona arelação existente entre a demanda de certo produto, bem ou serviço com a quantidade que é oferecida, tambémchamada de oferta. A partir desta relação de demanda e oferta conseguimos descrever o comportamento de consumo de cada produto em seus respectivos períodos, quantidades e preços. Isto é perceptível, por exemplo, quando detectamos que a demanda de um produto, em certo período, recebeu um aumento significativo em sua procura, fazendo com que seu preço tenda a cair. Já em períodos nos quais a demanda passa a superar a oferta, a tendência é o aumento do preço.
Para exemplificar esta teoria, podemos observar o gráfico que mostra a relação existente entre o preço do produto e a quantidade demandada. A curva tem inclinação positiva, ou seja, um preço maior (ou menor)corresponde a uma quantidade demandada menor (ou maior), isso deve-se ao fato por existir a lei da demanda.
A relação entre o preço e a quantidade ofertada é dada pela lei deoferta: quando o preço de um bem aumenta, com o restante permanecendo constante, a quantidadeofertada do bem também aumenta. No gráfico abaixo, vemos a inclinação positiva, neste caso se o preço é alto a quantidade ofertada também será alta.
Teoricamente, quando a relação de oferta e demanda se encontram estáveis, consequentemente, haverá uma estabilização do preço de venda. Mas como no mercado atual as empresas estão se tornando mais competitivas, sempre procurando reduzir seus custos para oferecer um produto com menor preço possível, acontece um desequilíbrio nas relações de oferta e demanda, provocando alterações no preço devido há existência de uma concorrência.
Observando o gráfico acima descreve o modelo da oferta e demanda. O gráfico mostra um aumento na demanda de D1 para D2 e o consequente aumento no preço e na quantidade necessário para se atingir um novo ponto de equilíbrio na curva de oferta (S).
Quando há uma procura maior por um determinado produto sem o preço variar a curva de demanda se desloca para a direita, de Do;Do para D1D. Aumenta aquantidade demandada do pelo maior consumo que este sofre.
E, em caso contrário, quando a procura de um produto diminui a curva de demanda se desloca para a esquerda de DoDo para D2D2.
Da mesma forma que a oferta exerce uma influência sobre a procura dos consumidores, a frequência com que as pessoas buscam determinados produtos também pode aumentar e diminuir os preços dos bens e serviços.
Mesmo observando a relação da demanda com o preço, devemos levar em consideração que a variação da demanda não depende exclusivamente da variação do preço. Existem outros elementos que também influenciam diretamente no comportamento da demanda, como, o desejo e a necessidade das pessoas, o poder de compra, a concorrência, a tecnologia, a existência de produtos complementares e substitutos.
- Modelo Matemático
Para representação matemática da pesquisa sobre os produtos que influenciam na quantidade demandada de farinha de mandiocautilizou-se o modelo matemático seguinte:
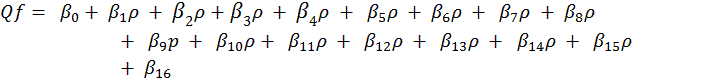
Em que:
Qf é a quantidade demandada de farinha de mandioca;
![]() é intercepto da equação;
é intercepto da equação;
![]() representa as inclinações da equação
representa as inclinações da equação
Aplicação do modelo Matemático
A representação simplificada da realidade, segundo a estrutura conceitual pede uma estimação de regressão múltipla , dada a quantidade de variáveis que influenciam na quantidade demandada de farinha de mandioca. Para efeito didático de instrumentalização da metodologia, o modelo adotado foi:
![]()
Onde as variáveis:
Qcf = Quantidade demandada de farinha mandioca;
(arr) = Quantidade demandada de arroz;
(prf) = Preço da farinha;
(mac) = Quantidade demandada de macarrão;
(cab) = Quantidade demandada de carne bovina;
(cas) = Quantidade demandada de carne suina;
(caf) = Quantidade demandada de carne de frango;
(pei) = Quantidade demandada de peixe;
(ovo) = Quantidade demandada de ovo;
(sar) = Quantidade demandada de sardinha;
(cac) = Quantidade demandada de carne em conserva;
(jab) = Quantidade demandada de jabá;
(aca) = Quantidade demandada de açaí;
(des) = Despesa familiar mensal com alimentação;
(ren) = Renda mensal familiar;
(qtp) = Quantidades de pessoas na família;
- Modelo Econométrico
Para o modelo ser validado foi adotado que as variáveis tenham valor de significância menor que 10%, ou seja, espera-se que haja 10% ou menos de chances das variáveis não serem significantes para o modelo. O software gerou a seguinte tabela após o tratamento dos dados:
DependentVariable: QTDEFARINHA |
||||
Method: LeastSquares |
||||
Date: 05/18/12Time: 19:35 |
||||
Sample(adjusted): 1 313 |
||||
Includedobservations: 213 |
||||
Excluded observations: 100 after adjusting endpoints |
||||
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
ARROZ |
0.733500 |
0.881302 |
0.832291 |
0.4063 |
PRECOFARINHA |
-0.685627 |
0.823687 |
-0.832388 |
0.4062 |
MACARRAO |
4.265981 |
1.076361 |
3.963338 |
0.0001 |
FEIJAO |
-2.371096 |
0.769994 |
-3.079372 |
0.0024 |
CARNEBOVINA |
0.245106 |
0.159467 |
1.537035 |
0.1259 |
CARNESUINA |
0.183911 |
0.104849 |
1.754056 |
0.0810 |
CARNEFRANGO |
-0.798510 |
0.235989 |
-3.383670 |
0.0009 |
PEIXE |
0.050018 |
0.103465 |
0.483424 |
0.6293 |
OVO |
0.151856 |
1.518705 |
0.099990 |
0.9205 |
SARDINHA |
-0.682697 |
0.363236 |
-1.879485 |
0.0617 |
CARNECONSERVA |
1.075434 |
0.515204 |
2.087396 |
0.0381 |
JABA |
0.211015 |
0.125275 |
1.684411 |
0.0937 |
ACAI |
-0.282586 |
0.157549 |
-1.793644 |
0.0744 |
DESPESA |
0.002460 |
0.001212 |
2.030387 |
0.0437 |
RENDA |
-0.000455 |
0.000128 |
-3.565461 |
0.0005 |
QTDEPESSOAS |
0.877917 |
0.264434 |
3.319984 |
0.0011 |
R-squared |
0.335577 |
Meandependent var |
5.890376 |
|
Adjusted R-squared |
0.284987 |
S.D. dependent var |
6.719923 |
|
S.E. ofregression |
5.682264 |
Akaikeinfocriterion |
6.384723 |
|
Sum squaredresid |
6360.760 |
Schwarz criterion |
6.637214 |
|
Log likelihood |
-663.9730 |
F-statistic |
6.633199 |
|
Durbin-Watson stat |
1.642412 |
Prob(F-statistic) |
0.000000 |
|
Observa-se na tabela que, no caso de aceitarmos variáveis com o nível de significância abaixo de 10%, serão excluídas do modelo as seguintes variáveis: quantidades de arroz, macarrão, feijão, carne suína, peixe, ovo, sardinha, carne conserva, jabá, a renda, a despesa e a quantidade de pessoas.
O R² (R-squared), segundo o software é igual a 0,335577, então as variáveis explicam em 33,55% a variação da demanda da farinha de mandioca. O R² é o coeficiente de determinação que mede a qualidade do modelo econométrico em relação a sua habilidade de estimar corretamente os valores das variáveis.
O R² ajustado (Adjusted R-squared) indica quanto o modelo explica a variável dependente excluindo as variáveis com pouco poder explicativo. O R² ajustado é igual a 28%.
Analisando a distribuição normal, percebe-se a falta de normalidade da série. O teste de Jarque-Bera foi igual a 339.1742, este teste avalia a hipótese de que determinada variável tem distribuição normal com média e variância especificada e a hipótese de que essa variável não tenha distribuição normal. Como o Jarque-Bera é maior que 5%, rejeita-se a distribuição normal da série. Outros indicadores como o coeficiente de simetria (Skewness) e o coeficiente de achatamento (kurtosis) mostram que o modelo não segue uma distribuição normal.
Um novo modelo foi estimado, excluindo-se as variáveis que estão com um nível de variância de significância maior que 10%. Restando então, apenas 6 variáveis. O software EVIEWS utilizou a seguinte equação:
![]()
Onde as variáveis:
Qcf = Quantidade demandada de farinha mandioca;
(c) = Constante
(aca) = Quantidade demandada de açaí;
(cab) = Quantidade demandada de carne bovina;
(caf) = Quantidade demandada de carne de frango;
(fat) = Quantidade demandada de farinha de tapioca;
(prf) = preço da farinha de mandioca;
Com a nova equação, o software gerou a seguinte tabela.
Dependent Variable: FARINHA_KG01 |
||||
Method: Least Squares |
||||
Date: 06/21/12 Time: 18:36 |
||||
Sample: 1 366 |
||||
Included observations: 366 |
||||
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
0.019693 |
0.219307 |
0.089797 |
0.9285 |
ACAI_LT01 |
0.157142 |
0.054137 |
2.902672 |
0.0039 |
CARNE_BOVINA_KG0 |
0.239429 |
0.076780 |
3.118377 |
0.0020 |
CARNE_DE_FRANGO_ |
0.269717 |
0.072396 |
3.725600 |
0.0002 |
FARINHA_TAPIOCA0 |
0.142663 |
0.069551 |
2.051205 |
0.0410 |
PRE01 |
-0.220769 |
0.136742 |
-1.614495 |
0.1073 |
R-squared |
0.208052 |
Mean dependent var |
1.407020 |
|
Adjusted R-squared |
0.197053 |
S.D. dependent var |
0.920410 |
|
S.E. of regression |
0.824755 |
Akaike info criterion |
2.468797 |
|
Sum squared resid |
244.8794 |
Schwarz criterion |
2.532774 |
|
Log likelihood |
-445.7898 |
F-statistic |
18.91504 |
|
Durbin-Watson stat |
1.416764 |
Prob(F-statistic) |
0.000000 |
|
Com isso, a partir dos coeficientes obtidos pelo software é possível definir a equação como:
Qf = c + 0,1571aca + 0,2394cab + 0,2697caf + 0,1426fat – 0,2207prf
As variáveis quantidade de açaí, quantidade de carne bovina, quantidade de carne de frango, quantidade de farinha de tapioca e preço da farinha de mandioca explicam em 20,80% a variação da quantidade demandada de farinha de mandioca, de acordo com o indicador R² (R-squared) que é igual a 0,208052. O R² ajustado diz que o modelo explica 19,70% a variação da variável dependente.
Observa-se na nova distribuição normal uma maior simetria das variáveis. Os dados estão distribuídos normalmente na série. Segundo os Jarque-Bera = 3.259510, que é menor que 5%, o modelo de distribuição é válido. Seguindo os indicadores de Skewnesse Kurtosisa distribuição normal também é valida.
- Validação do Modelo
Como já foi mostrado, agora é possível afirmar que todas as variáveis são significativas estatisticamente ao nível de 10%, podendo-se, então interpretar teoricamente os dados utilizados.
Para validar o modelo foi utilizada a fórmula (100 x Valor-P) £ 10%, podendo-se aceitar as hipóteses alternativas de que as variáveis exercem influência na quantidade demandada de farinha de mandioca.
- Testes de Validação de Hipóteses
- Teste de Heterocedasticidade
White Heteroskedasticity Test: |
|||
F-statistic |
1.232452 |
Probability |
0.224419 |
Obs*R-squared |
24.40571 |
Probability |
0.225119 |
Percebe-se que a presença de homoscedasticidade é garantida, uma vez que, por meio do teste F, o valor da probabilidade é maior que 10% (valor de significância estabelecido). Assim pode-se dizer que os estimadores e parâmetros são altamente significativos, os desvios-padrão são corretos, as estatísticas T e F não são viesados e perfeitamente reais.
- Teste de autocorrelação
Autocorrelação significa dependência temporal dos valores sucessivos dos resíduos, ou seja, os resíduos são correlacionados entre si. Em termos formais, considerando o modelo linear
Yt=a + bx + et, a autocorrelação significa, portanto,:
E(eiej)= 0 para i diferente de j.
Quando os resíduos são autocorrelacionados, as estimativas de mínimos quadrados ordinários dos parâmetros não são eficientes , isto é, não apresentam variância mínima, além de seu erro-padrão ser viesado, o que conduz a testes e intervalos de confiança incorretos. Se a auto correlação for positiva, os erro-padrões serão substimados e, consequentemente, os valores da estatística t, superestimados. Se a autocorrelação for negativa, os erro-padrões serão superestimado e o valor da estatística t, subestimado.
Portanto a autocorrelação positiva é mais danosa, porque existirá, no caso do teste “t” , o risco de rejeitar-se a hipótese nula de ausência do efeito, quando deveria aceita-la.
A autocorrelação é positiva quando os resíduos são diretamente relacionados entre si:
et = ret-1+ vt’ r > 0
Quando r < 0 , a autocorrelação é negativa.
Tal correlação é dita de primeira ordem, porque o resíduo et é relacionado com o et-1, ou seja, o resíduo em t é função do resíduo no período imediatamente anterior (t-1).
Dentre os procedimentos estatísticos existentes para determinar se os termos erro são não-correlacionados, vamos utilizar o teste Durbin_Watson. O resultado encontrado foi 2.040581
O valor calculado de d é comparado com os limites inferior (di) e superior (du) de valores, tabelados por Durbin_Watson. Portanto para o modelo de regressão linear múltipla da demanda de carne de frango tem-se o resultado de autocorrelação positiva, ou seja, dl> d > 0.
Referencias
SANTANA, A. C. et al. Estudo exploratório sobre a dinâmica de produção e agroindustrialização de frango no Brasil e Região Norte. Belém: BASA; FCAP, 1995.
CORRAR, L.; PAULO, E.; DIAS FILHO, J. Análise Multivariada para os Cursos de Administração, Ciências Contábeis e Economia. São Paulo: Atlas, 2007.
SANTANA, A; C. Elementos de economia, agronegócio e desenvolvimento local. Belém: GTZ; TUD; UFRA, 2005.

