Introducción

Se sabe por Carlos Marx y otros economistas, que el pensamiento económico adquiere su fundamento científico como ciencia con sus principales representantes: Adam Smith, David Ricardo y Roberto Malthus. Cada uno de ellos enfoca el problema económico a partir de la reproducción de los factores de producción. Para esto, utilizaban instrumentos como la teoría del salario sin considerar el problema de la escasez relativa del trabajador, la teoría de la población y su reproducción, y la reproducción continua del mismo aparato productivo; es decir, que los factores productivos gastados tienen que ser remplazados y por tanto reproducidos.
Desde ese surgimiento de la economía como ciencia, se vuelve relevante para comprender la realidad, la utilización de modelos económicos(sean estos teóricos y/o matemáticos), los cuales son una representación simplificada de la realidad. De acuerdo a los clásicos la construcción de modelos económicos requiere la utilización de tres supuestos: simplificadores, fundamentales y tendenciales. Los simplificadores como su nombre lo indica tratan de simplificar la realidad aunque a veces no contrasten con ella; los fundamentales pueden operar en la realidad y son efectivos; y los tendenciales son supuestos que aparentemente no existen, pero que es necesario agregárselos al modelo para que este funcione.
Desde los economistas clásicos1 a la fecha, han aparecido diferentes escuelas de pensamiento económico: la escuela Cambridge, Lausana, de Chicago, keynesiana, la síntesis neoclásica, los monetaristas, los neos keynesianos y los institucionalistas entre otras; las cuales han tratado de explicar la teoría económica utilizando modelos económicos ya sean los anteriores u otros para realizar análisis microeconómico y/o macroeconómico. 
Así, la escuela (o teoría) neoclásica es una de ellas, la cual centró su atención en la optimización y asignación eficiente de los factores productivos, para ello, puso especial atención en la asignación del capital; dicha escuela enfoca el problema de los factores de producción desde el punto de vista de la asignación optima de los recursos escasos ante necesidades ilimitadas de la economía o de la sociedad.
Para ellos el valor de los factores de producción debe de ser igual a su remuneración o coste. Por ejemplo, el Producto Marginal del Trabajo (PMgL) multiplicado por vector Precio (P) debe ser igual al salario (w): PMgL* P = w. Lo cual indica que el PMgL debe ser igual al salario real (w/P). De igual manera consideran al capital como una variable de flujo, la cual solo se puede conseguir si el vector precio de la economía y la tasa de beneficios (tasa de interés “i”) se conocen de antemano: PMgL* P = i.
En tal sentido, el objetivo central de esta investigación bibliográfica es: “criticar la función de producción agregada neoclásica, particularmente la función Coob-Douglas, de Solow y la CES, sus problemas de agregación de factores de producción y modelos de crecimiento utilizados en el análisis macroeconómico”.

Se concluye que la función de producción neoclásica, sus formas de agregación de los factores productivos y sus modelos de crecimiento económico utilizados están amplia y profundamente objetados.
Como es costumbre, el presente ensayo se expone de la forma siguiente: el objetivo, la definición, justificación e hipótesis general sobre la función de producción neoclásica; la metodología bibliográfica utilizada; se continua con la exposición de la contabilidad del crecimiento que incluye el residuo de Solow, el caso general de la Constante Elasticity of Sustitution (CES) y la función de producción Cobb-Douglas; inmediatamente se incorporan las valoraciones o críticas más importantes que han hecho hasta ahora a estos modelos de crecimiento económico neoclásico. Se finaliza con una serie de bibliografía que sustenta las argumentaciones anteriores.

Objetivo de la Investigación.

Valorar la función de producción agregada neoclásica, particularmente la función Coob-Douglas, de Solow y la CES, sus problemas de agregación de factores de producción y modelos de crecimiento utilizados en el análisis macroeconómico.

Definición de la problemática

Los modelos de crecimiento económico neoclásicos se estructuran acordes a una función de producción agregada, que partiendo de supuestos, premisas y axiomas razonados satisfacen la lógica matemática; sin importar que éstos sean reales o ficticios para la económica.

Justificación

En las funciones de producción agregadas neoclásicas del tipo:, donde Q es el producto físico único y homogéneo, L es el trabajo y K es el capital, la economía neoclásica llega a tres resultados: 1) la tasa de beneficio real del capital (la tasa de interés) está determinada por las propiedades técnicos de la productividad marginal decreciente del capital; 2) una mayor cantidad de capital conlleva un menor producto marginal del capital adicional, y por tanto, una menor tasa de interés; y 3) la distribución del producto entre trabajadores y capitalistas se explica por la abundancia relativa de los factores y por los productos marginales. Así, el precio de los servicios del capital (la tasa de interés) está determinado por la escasez relativa y la productividad marginal del capital agregado; el precio de los servicios del factor trabajo (el salario) está determinado por la escasez relativa y la productividad marginal del trabajo. (Felipe, J. y McCombie, 2005:47, basándose en Cohen y Harcut, 2003).

Por eso la teoría neoclásica agregada, según Shaikh, ha sido formulada a menudo mediante la analogía con la correspondiente teoría microeconómica, con la justificación de que los modelos de equilibrio general son inútiles, a menos que sean muy simplificados. Sin embargo, las recientes controversias (véase a Felipe, Jesús y McCombie, J.S.L., 2004; Felipe, Jesús y McCombie, J.S.L., 2005; Felipe, Jesús y Fischer, Franklin, 2004; y Felipe, Jesús y McCombie, J.S.L., (2012) sobre el capital han aclarado las condiciones que requieren las funciones de producción «sustitutas» («surrogate»), y estas condiciones se reducen a que en cualquier momento rija en la economía una simple teoría del valor trabajo. La ironía de este resultado no puede pasar inadvertida; además, este resultado implica que muchos economistas deben escoger un difícil camino, al repudiar un sistema de determinación de precios mediante la teoría del valor trabajo, aceptando, sin embargo, sus conclusiones, ya que el uso de tales funciones, tanto en la investigación teórica como en la empírica, está muy difundido. La explicación de esta popularidad parece estar en el hecho de que la base empírica del análisis de las funciones agregadas de producción es una base sólida. Pero no cualquier función, puesto que tanto en los análisis «cross-section» como en los estudios de series históricas, la función Cobb-Douglas aparece por encima de las demás: «la suma de los coeficientes generalmente está cerca de lo unidad y existe una sorprendente semejanza entre el exponente de la variable trabajo y la participación de los salarios en producto total». Por ello, parecería que los resultados empíricos apoyan tanto las funciones de producción agregadas con rendimientos constantes, como la teoría agregada marginal de la distribución, casi a pesar de sus deficiencias teóricas.
F. Fisher, continua Shaikh, admite que los supuestos «bajo los que las posibilidades de producción de una economía técnicamente se pueden representar por una función de producción agregada, son demasiado limitativos para ser verosímiles». Por tanto, propone que se investigue la sorprendente uniformidad de los resultados empíricos mediante un experimento de simulación: se supone que cada una de las N industrias de la economía está caracterizada por una función de producción microeconómica Cobb-Douglas que relaciona su producto (homogéneo) con su trabajo (homogéneo también) y su stock de maquinaria, diferenciado. Las condiciones de agregación son violadas premeditadamente, y la pregunta que se hace entonces es hasta qué punto, y bajo qué circunstancias, una función de Cobb-Douglas agregada representa los datos obtenidos. En una economía como ésta, la participación agregada de los salarios a menudo varia con el tiempo, con lo que, en general, una función de producción de tipo Cobb-Douglas no se podrá ajustar. Sin embargo, lo que parece sorprender a Fisher es que, cuando la participación de los salarios es por casualidad constante, una función de producción Cobb-Douglas, no solamente se ajusta a los datos, sino que también proporciona una explicación de los salarios «aunque las verdaderas relaciones estén lejos de ajustarse a una función Cobb-Douglas», sugiriendo con ello que «La opinión que mantiene que la constancia de las participaciones relativas se debe a la presencia de una función de producción Cobb - Douglas agregada, está equivocada. La línea de causalidad va en sentido opuesto y el aparente éxito de la función Cobb-Douglas se debe a la constancia relativa de la participación del trabajo» (Véase a Shaikh, Anwar (s/f: 343/354).

Hipótesis General

Las funciones de producción agregadas, tipo Cobb-Douglas, de Solow y CES en particular, son más identidades contables y ecuaciones matemáticas que cumplen con las propiedades siguientes: son homogéneas de primer grado, sus derivadas parciales son iguales a los salarios y beneficios; y el tercero, es el efecto del tiempo aparece como neutral.

Metodología

El abordaje de este ensayo es eminentemente bibliográfico reflexivo. En un primer momento se procedió a realizar una compilación de información bibliográfica referida a la estructura y funcionamiento de la función de producción agregada y de sus modelos econométricos. Todos estos documentos fueron leídos, comentados y analizados por los investigadores.
Posteriormente, se realizaron cinco puestas en común entre el grupo de investigadores, en las cuales se discutió sobre la existencia o no de  fallas en el modelo de crecimiento basado en la función de producción agregada. Luego de haber discutido y consensuado, se procedió a la sistematización y redacción del presente artículo.   

La contabilidad del crecimiento

De la contabilidad del crecimiento, se tiene que las causas del crecimiento, según Dornbusch, R., Fischer, S. y Startz, R. (2004: 57 – 80), se expresan en la función de producción (1) siguiente:

La producción crece con los aumentos de los factores de producción (K, N) y con los incrementos de la productividad provocados por la mejora de la tecnología y de la capacitación de la mano de obra (A).
Así, la función de producción (1) establece una relación cuantitativa entre los factores y los niveles de producción.  Por eso, la función (1) muestra que la producción (Y) depende de los factores (K, N) y del nivel de tecnología (A), siendo los factores (K) Capital y (N) trabajo. Donde A representa el nivel de la tecnología porque cuanto mayor es, más producción se obtiene con un nivel dado de factores; a veces A se denomina “productividad”, que es un término más neutral que “tecnología”.
Por lo tanto, más producción significa más uso de factores. En otras palabras, el producto marginal del trabajo (PMN), que se define como el aumento de la producción generado por un incremento del trabajo; y el producto marginal del capital (PMK), que se define como el aumento de la producción generado por un incremento del capital, son ambos positivos.
Así, la ecuación (1) relaciona el nivel de producción con el nivel de factores y el nivel de tecnología. A menudo es más fácil trabajar con tasas de crecimiento que con niveles. Esta función de producción (1), puede transformarse en una relación muy específica entre el crecimiento de los factores y el crecimiento de la producción, que se resume por medio de una ECUACION DE LA CONTABILIDAD DEL CRECIMIENTO. Para pasar de la ecuación (1) a la ecuación (2), se necesita el SUPUESTO de que la economía es COMPETITIVA.

Para llegar a la ecuación (2), se puede hacer la pregunta siguiente:
¿Cuánto varía la producción (ΔY) si el trabajo varía en ΔN, el capital varía ΔK y la variación de la productividad en ΔA o productividad total de los factores (provocados por la mejora –que es equivalente a más - de la tecnología y la capacitación de la mano de obra)?.Así, la variación de la producción será:

Donde: PMN = producto marginal del trabajo (N ó L) y PMK = producto marginal de capital (K). Dividiendo los dos miembros de esta ecuación (2.1)  por Y = AF(K,N) y simplificando se obtiene (2.2):


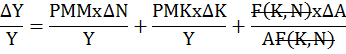
Ahora, se multiplica y divide el primer término de la derecha por N y el segundo por K de (2.2), de donde se obtiene la ecuación anterior (2) siguiente.

De ahí se supone que la ecuación (2), es para una economía competitiva. En una economía competitiva, los factores de la producción perciben su producto marginal. Por lo tanto, PMN = w, donde w es el salario real. El pago total del trabajo es el salario multiplicado por la cantidad de trabajo, won; el pago total del trabajo en proporción de todos los pagos –es decir, la “participación del trabajo” - es: (el mismo argumento se utiliza para el caso del capital).
Por lo tanto, si ahora se sustituye:
 =  y .. .                          . Y, .
Se obtendrá la ecuación (3) 1 siguiente:

La ecuación (3) significa que, el crecimiento de la producción (Y) es atribuible a la participación de los factores trabajo (N ó L), capital (K) y al progreso tecnológico o productividad de los factores (A). Así, i) el trabajo y el capital contribuyen en un monto igual a sus tasas individuales de crecimiento multiplicadas por la participación de ese factor en el ingreso; e ii) la medida del adelanto tecnológico, progreso técnico o crecimiento de la productividad de los factores. Por lo tanto, la tasa de crecimiento de la productividad total de los factores es el monto en que la producción se incrementaría como resultado de adelantos en los métodos de producción, sin que cambien los factores.
Dado que ese crecimiento debe reflejarse en el bienestar individual, la ecuación (3) se expresa en términos de ingreso promedio per cápita (es el cociente entre el PIB y la población), así:

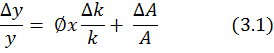
El numero de maquinas por trabajador (k), que también se llama razón de capital a trabajador, determina el monto de la producción que puede generar cada trabajador.
Igualmente, de (3) se deduce, el residuo de Solow siguiente.

El residuo de Solow

¿Cómo se mide el progreso técnico?. Según (Dornbusch, Fischer y Start, 2004: 62), por definición, las variaciones de A explican todas las variaciones de la productividad que no se deben a variaciones de los factores. Las variaciones de A se denominan a veces variaciones de la productividad total de los factores (PTF), términos más neutros que “progreso técnico”. Dado que los factores y los productos son observables directamente, pero no así A, se procede a medir ∆A/A dándole la vuelta a la ecuación (3), así (3.1):

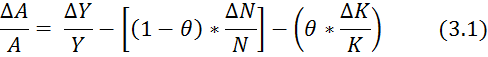
En (3.1), se atribuye todo lo que queda a la izquierda a las variaciones de la PTF, que medidas de esta forma, se denominan residuo de Solow.
Por su parte (Cabrera, 2003:36-39), suponiendo rendimientos constantes a escala (RCE) y partiendo del mismo argumento de Solow (1957), concluye con la ecuación (3.2) siguiente:

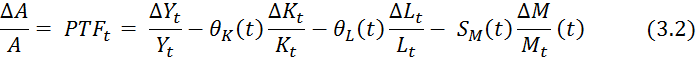
Donde, son las participaciones del capital, trabajo e insumos intermedios en la producción bruta. Si A varía, tiene que haber algún progreso (o retroceso) técnico. Entonces, el grado de progreso técnico o crecimiento de la Productividad Total de los Factores (ΔPTF), se mide por medio de la diferencia entre el primer miembro de la ecuación (3.2) y el segundo; y el crecimiento de la PTF es positivo cuando la producción bruta crece más rápido de lo que crecen los factores y los insumos.
Hay que considerar algunas similitudes y diferencias entre la ecuación (3.1) y (3.2). Las similitudes son que ambos asumen que hay competencia y rendimientos constantes a escala y por lo tanto las elasticidades de los factores podrían ser iguales a 1. La diferencia es que la (3.2), incluye como otro factor a los insumos (por ejemplo materias primas, materiales auxiliares, etc.).
Por otro lado, Cabrera (2003:9), considera que la PTF se relaciona directamente con el ciclo de los negocios, por lo que es deseable analizar el crecimiento y la PTF libre de oscilaciones cíclicas con el fin de deducir el crecimiento a largo plazo. Esto lo conduce a la estimación de la frontera o curva de posibilidades de producción, que es de donde se estiman las desviaciones de una unidad productiva (empresa, rama de producción o economía) que se supone eficiente2 con relación al resto de unidades productivas que no son eficientes; y estas fronteras pueden calcularse respecto a los insumos o productos. La primera calcula los insumos necesarios para producir un determinado nivel de producción; y la segunda, pretende la máxima cantidad de producción en función de los insumos dados 3.
En tal sentido, en la teoría moderna de crecimiento económico basada en fronteras estocásticas de producción, las variables que se incorporan como explicativas a las diferencias en la eficiencia (en la productividad total de factores) están: variables geográficas; históricas, políticas y culturales; y variables que dependen de la política económica y social. Concretamente (Cabrera, 2003:9), plantea que uit (como variable estocástica e independiente) representa la ineficiencia económica que la evalúa considerando las variables explicativas siguientes: el crowdingout medido por el déficit del gobierno general respecto al PIB (GDP), el capital humano (H) medido por la porción de la población adulta (entre 25 años y más) que han completado educación secundaria, el desarrollo financiero (DF) medido por la importancia relativa de los depósitos bancarios respecto a los activos del Banco Central, la apertura de la economía (OPEN) medido por la ratio de las exportaciones mas las importaciones de bienes y servicios respecto al PIB, y agrega una variable DUMMY por países y temporal para captar las crisis políticas sociales individuales que hayan desembocado en conflictos militares.
Por lo tanto,  la frontera de eficiencia representa el máximo nivel de producción que se puede obtener si se emplean los factores productivos a plena capacidad con una tecnología dada. La ineficiencia técnica corresponde a diferencias entre ese máximo teórico y lo que en efecto produce una economía dado un nivel de insumos.

El caso general. La función de producción de Constant Elasticity of Substitution (CES)

Por otro lado, la función de producción CES (constant elasticity of substitution o elasticidad de sustitución constante o rendimientos constantes) es el caso general de la función de producción Cobb-Douglas.
Así, se ha generalizado el uso de la función de producción que, aun cuando se caracteriza por una CES, puede proporcionar una σ (letra griega minúscula “sigma” que significa elasticidad de sustitución) con un valor (constante) diferente1 de 1. La ecuación de esta función de producción es la CES (Chaing, A. C, y Wainwright, 1967:397 - 399), y es la siguiente (4):

Donde K (capital) y L (trabajo) representan dos factores de producción, y A, δ (letra griega minúscula “delta”) y ρ (la letra griega minúscula “rho”) son tres parámetros. El parámetro A (el parámetro de eficiencia) juega el mismo papel que el coeficiente A en la función de Cobb - Douglas; sirve como indicador del estado de la tecnología. El parámetro δ (el parámetro de distribución), al igual que la α (alpha) ó θ (letra griega minúscula “theta”) en la función de Cobb- Douglas, tiene que ver con las participaciones del factor relativo en el producto. Y el parámetro ρ (es de sustitución) — que no tiene equivalente en la función de Cobb - Douglas — es lo que determina el valor de la elasticidad de sustitución (constante).
Sin embargo, obsérvese primero que esta función (4) es homogénea de grado uno. Si se reemplaza a K y L por jK y jL, respectivamente, el producto va a cambiar de Q a (5):

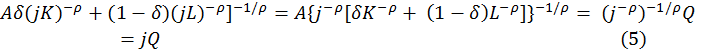
En consecuencia, la función CES, al igual que todas las funciones de producción linealmente homogéneas, exhibe retornos constantes de escala, califica para la aplicación del teorema de Euler 2, y posee productos promedios y productos marginales que son homogéneos de grado cero en las variables K y L.
Se puede también observar que las isocuantas generadas por la función de producción CES siempre tienen pendiente negativa y son estrictamente convexas para los valores positivos de K y L. Para mostrar esto, se encuentran primero las expresiones para los productos marginales QL y QK. Usando la notación […] como una abreviatura para ], se obtiene (6):

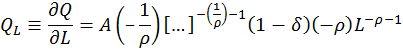
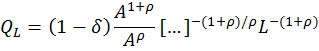
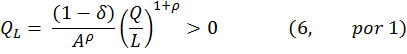
y en forma similar (7),

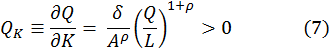
Que se definen para los valores positivos de K y L. Entonces, la pendiente de las isocuantas (con K graficado en sentido vertical y L en sentido horizontal) es (8):

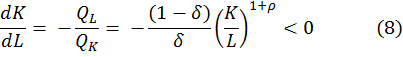
Para (8), pueden verse las condiciones de primer orden para la maximización de ganancia.
Entonces, puede verificarse fácilmente que , lo que implica que las isocuantas son estrictamente convexas para K y L positivos.

También puede mostrarse que la función de producción CES es estrictamente cuasicóncava para K y L positivos. La diferenciación adicional de (6) y (7) muestra que las segundas derivadas de la función tienen los siguientes signos (9):





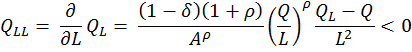
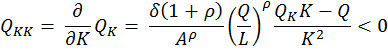
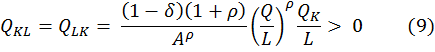
Estos signos de las derivadas, válidos para K y L positivos, permiten verificar la condición suficiente para la cuasiconcavidad estricta. Como se puede verificar en (10),


Entonces, la función CES es estrictamente cuasicóncava para K y L positivos.
Por último, se usaran los productos marginales de (6) y (7) para encontrar la elasticidad de sustitución de la función CES. Para satisfacer la condición de combinación de costo mínimo QL / QK = PL /PK, donde PL y PK denotan los precios del servicio laboral (tarifa del salario) y el servicio del capital (cargo de la renta por los bienes de capital), respectivamente debemos tener (11)

Entonces, la relación óptima de insumos (introduciendo el símbolo c para abreviar), será (12)

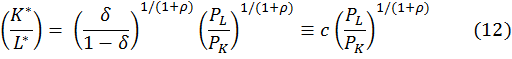
Tomando a (K* / L*) como una función de (PL / PK), se encuentra que las funciones asociadas marginal y promedio son (13).

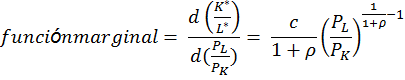
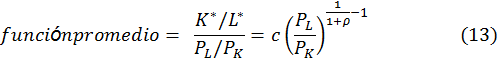
Por lo tanto, la elasticidad de sustitución será 1 (14)

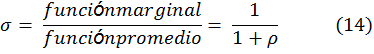
Lo que muestra esto es que  es una constante cuya magnitud depende del valor del parámetro , como se muestra en (15):

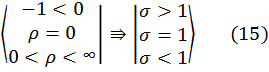
Entonces, que σ sea mayor, igual o menor que 1, dependerá del grado de elasticidad de sustitución que presenten los factores en el proceso de producción.

La función de Cobb - Douglas como un caso especial de la función CES

En este último resultado (15), el caso medio de  conduce a una elasticidad de sustitución unitaria que, como se sabe, es característica de la función de producción Cobb - Douglas. Esto sugiere que la función de Cobb - Douglas (linealmente homogénea) es un caso especial de la función CES (linealmente homogénea). La dificultad es que la función CES, como está dada en (4), es indefinida cuando , ya que la división por cero no es posible. Sin embargo, se puede demostrar que, cuando , la función CES se aproxima a la función Cobb-Douglas.
Para esta demostración, se emplea una técnica conocida como la regla de L’Hópital. Esta regla tiene que ver con la evaluación del límite de una función como  , cuando   (donde “a” puede ser finito o infinito), cuando el numerador m(x) y el denominador n(x) son: (1) ambos tienden a cero cuando , lo que conduce a una expresión de la forma 0/0; y (2) ambos tienden a  cuando  , conduciendo así a una expresión de la forma  (ó , ó ). Aun cuando el límite de  no puede evaluarse tal como está la expresión en estas dos circunstancias, no obstante su valor puede encontrase usando la fórmula (16) siguiente (regla de L’Hospital).

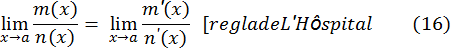
Dado que la función de producción Cobb – Douglas es un caso particular, a los economistas neoclásicos y/o neoliberales les atrae la función Cobb – Douglas porque, según ellos “describe de una manera relativamente exacta la economía 1 y es muy fácil de utilizar algebraicamente” (Dornbusch, Fischer y Startz, 2004:59). La función de producción Cobb – Douglas es la función (17):

Para el caso de los USA, se ha encontrado que,  para el capital (K) y el trabajo (N) respectivamente.

Además, (17) significa que presenta Rendimientos Constantes de Escala (RCE), los que significa que si todos los factores aumentan en la misma proporción, la producción aumenta en la misma proporción. En términos matemáticos, si multiplicamos ambos factores por una constantes c, la producción también se multiplicara por c: AF (cK, cN) = cAF (K, N) = cY. El argumento es creíble, dicen Dourbusch,.., debido al argumento de la duplicación: si una fábrica que utiliza X trabajadores produce Y, dos fábricas que utilicen X trabajadores cada una deberán producir 2Y; tres que utilicen X trabajadores cada una deberán producción 3Y, y así sucesivamente. Además de este atractivo argumento lógico, la evidencia empírica también sugiere que los RCE son más o menos constantes. Para demostrar que la función de producción Cobb – Douglas tiene RCE, multiplicamos tanto K como N por c:

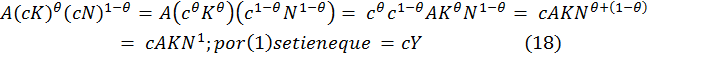
Para demostrar que la participación del capital es , multiplicamos el producto marginal del capital:

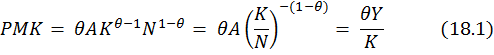
que es lo que percibe una unidad de capital en un mercado competitivo, por el número de unidades de capital utilizadas y si se divide por la producción total, se obtiene (19):

Donde efectivamente, el exponente  de la función Cobb – Douglas en (19) es el mismo  que aparece en la ecuación de la contabilidad del crecimiento (3).

Consideraciones sobre la función de Cobb – Douglas, el modelo de Solow y la función CES

Sobre estas funciones de producción neoclásicas anteriormente expuestas, algunos autores han concluido lo siguiente:

Para Hayek (2007:13), por ejemplo, manifiesta que en lo que respecta a Jevons y Walras, se pensaba, con razón o sin ella, que lo radicalmente nuevo de sus aportaciones era el método matemático, no el contenido de sus teorías, y éste fue justamente el obstáculo principal de la aceptación respecto a la teoría de Karl Menger.
Según Marchal, esa economía neoclásica, es una ciencia económica, que tiene carácter exclusivamente especulativo. El investigador empieza a escoger – consciente e inconsciente - algunas premisas más o menos hipotéticas; sobre éstas, estructura un edificio científico, que es tenido por valido cuando satisface totalmente las exigencias de la lógica…con una sola condición que constituya una estructuración coherentes con las premisas; poco importa que las premisas sean conformes a la realidad o no; cualquier critica que denuncie únicamente un hiatos entre la hipostasis básica y los datos concretos, es una crítica mal lograda…pues las únicas criticas que valen son aquellas que se dirigen contra la rigurosidad lógica del razonamiento… El ideal de la teoría abstracta es elaborar un ciclo completamente lógico (Marchal, Adré, 1955:1/10).

Además, la teoría neoclásica se interesa principalmente por el consumo, la demanda y la utilidad. El concepto de utilidad marginal fue introducido para efectuar este cambio de los puntos considerados importantes, y desde entonces domina el pensamiento académico con autoridad casi indiscutida. Sin embargo, se le ha considerado no solo como una adición a la “caja de herramientas” de la economía, sino también como una innovación vital del método para tratar la ciencia (Rol, Eric, 1939).

Ese enfoque marginalista, dice Piero Sraffa, exige que la atención se centre en la variación, porque sin variación, bien en la escala de la industria, bien en «las proporciones de los factores de producción», no puede haber producto marginal ni coste marginal. En un sistema donde la producción continuara sin variación en esos aspectos, día tras día, el producto marginal de un factor (o, alternativamente, el coste marginal de un producto) no sólo sería difícil de encontrar, sino que no habría donde encontrarlo”. Además, “descansa sobre el supuesto tácito de rendimientos constantes en todas las industrias” (Sraffa, Piero, 1960:10/13).

Pero, los tres resultados identificados anteriormente en los cuales se fundamentan las funciones de producción neoclásicas, según Felipe y McCombie (2005), no se cumplen más que en el caso muy especial del modelo de un sólo producto; además de hacer desaparecer, como lo sostiene Joan Robison, dos conceptos históricos distintos del capital: uno, referido a capital como ahorro acumulado a través del tiempo (un fondo) o su concepto financiero del capital; y dos, capital como un conjunto de factores productivos, bienes de capital heterogéneos.

En lo que respecta al debate Cambridge-Cambridge, las partes concluyeron, según Felipe y McCombie (2005:52/54), que los problemas de recambio (reswitching) y la reversión del capital (capital reversing) eran posibles teóricamente y suponían graves problemas para la justificación del uso de las funciones de producción agregadas neoclásicas (por ejemplo, a nivel de sector), ni siquiera como “parábolas”. De ahí que estos modelos, incluyendo los endógenos, han dado lugar a una mala forma de hacer economía, y a consejos de política económica sin fundamento; ya que la función de producción agregada neoclásica es sin lugar a dudas el aparato más dudoso de la macroeconomía actual. Además, las implicaciones de las condiciones de agregación bajo las cuales las funciones de producción microeconómicas se pueden agregar para dar lugar a una función de producción agregada neoclásica serian las siguientes: 1) excepto en el caso de rendimientos constantes a escala, las funciones agregadas de producción muy posiblemente no existen; 2) incluso bajo el supuesto de rendimientos constantes, las condiciones de agregación son tan difíciles de satisfacer que hacen de la existencia de la existencia de la función de producción en economías reales la excepción y no la regla(esto incluye también los agregados de trabajo y producto); y 3) no se puede escapar de los anteriores resultados argumentando que las condiciones de agregación son aproximaciones satisfactorias, porque no se pueden derivar ni siquiera como una aproximaciones.

Así, las funciones de producción neoclásicas, no son más que aproximaciones a la identidad contable que relaciona el valor agregado con la masa salarial y los beneficios. Lo anterior implica que cualquier trabajo teórico o empírico basado en la función de producción agregada debe ser visto con grandes escepticismos y cautela (Felipe, J. y McCombie, J.S.L., 2005:83/84).
Por otro lado, la literatura sobre la agregación ha demostrado que las condiciones bajo las que una serie de funciones de producción microeconómicas pueden ser agregadas y generar la función de producción agregada son sumamente tan restrictivas y es difícil creer que las economías reales las satisfacen. Estos resultados cuestionan la legitimidad de los modelos de crecimiento neoclásicos y sus implicaciones. La conclusión es que si la economía neoclásica se precia de tener carácter científico alguno no puede evolucionar bajo la premisa falsa de que las funciones de producción agregadas existen. Por ello, la profesión debería reflexionar antes de continuar desarrollando modelos de crecimiento teóricos de corte neoclásico y haciendo trabajo empírico sin fundamento teórico sólido (Felipe, Jesús y Fischer, Franklin M., 2005:127/132).
Igualmente, Felipe y McCombie, concluyen al referirse a la Productividad Total de los Factores (TFP por sus siglas en inglés) que la naturaleza tautológica de las estimaciones de la TFP yace en el corazón de una cuestión importante que ha abordado la literatura empírica sobre el crecimiento económico durante los últimos años. Por lo tanto, sus argumentos son poner en duda la necesidad de esa teoría de la TFP (Felipe, Jesús y McCombie, J.S.L, 2007:195).
Y por si lo anterior fuera poco, Felipe y MacCombie, muestran que la función de producción regional neoclásica, los buenos ajustes estadísticos comúnmente encontrados empíricamente son únicamente debido al uso de datos de valor y una identidad subyacente de la contabilidad. El resultado es que las estimaciones obtenidas no pueden considerarse como evidencia de la estructura tecnológica subyacente de la economía espacial, incluyendo el agregado elasticidad de sustitución, el grado de rendimientos de escala y la tasa de progreso técnico (Felipe, Jesús y McCombie, 2012:1/2).
En tal sentido, argumenta Shaikh (s/f: 352), se demuestra que cuando los datos de la distribución (salarios y beneficios) presentan participación constante, existen amplios conjuntos de datos de producción (producto, capital y trabajo) que pueden siempre relacionarse mediante una forma funcional, matemáticamente idéntica a una Cobb-Douglas con «rendimientos a escala constantes», «progreso técnico neutral» y «productos marginales iguales a las retribuciones de los factores». Ya que lo anterior es una consecuencia matemática de las participaciones constantes, verdad oral incluso para un conjunto muy implausible de datos de producción (como los de un economía «embustera») se puede decir que la supuesta fuerza empírica de análisis de la función de producción no es en realidad nada más que un reflejo estadístico de la constancia de las participaciones de los factores (aún inexplicada).
En síntesis, se puede decir que la función de producción neoclásica, sus formas de agregar los factores productivos y los modelos de crecimiento económico utilizados, en la actualidad, están muy cuestionados; debido a que la agregación de los factores de producción no es homogénea sino heterogénea, los coeficientes encontrados para éstos en sus modelos de crecimiento corresponden igualmente tanto a una identidad contable como a una formulación funcional matemática idéntica a una función Cobb-Douglas, los cuales son ciertos incluso tratándose de teorías no económicas, y presentan igualmente rendimientos a escala constantes, progreso técnico neutral y productos marginales iguales a las retribuciones de los factores.

Conclusiones

Por lo tanto, las funciones de producción agregadas, tipo Cobb-Douglas, de Solow y CES en particular, son más identidades contables y ecuaciones matemáticas que cumplen con las propiedades siguientes: son homogéneas de primer grado, sus derivadas parciales son iguales a los salarios y beneficios; y el tercero, es que el efecto del tiempo aparece como neutral.
En tal sentido, los modelos de crecimiento económico neoclásicos se estructuran acordes a una función de producción agregada, que partiendo de supuestos, premisas y axiomas razonados satisfacen la lógica matemática; sin importar que éstos sean reales o ficticios para la economía.

Bibliografía

Branson, William H. (1972): “Teoría y política macroeconómica”. Fondo de Cultura Económica, México; segunda reimpresión de 1981.

Cabrera Melgar, Oscar Ovidio (2003): “Cómo crecer más rápido: El papel de la eficiencia económica como una explicación de las diferencias regionales de la productividad total de los factores”. Documento de Trabajo 2003-02, segundo semestre, Banco Central de Reserva de El Salvador.

Chiang, Alpha C. y Wainwright (1967): “Métodos fundamentales de economía matemática”. Edit. por Mc Grow Hill, cuarta edición de 2006.

Dornbusch, Rudiger; Fischer, Stanley y Startz, Richard (2004): “Macroeconomía”. McGrawHill, novena edic. de 2006, España.

Felipe, Jesus and McCombie, John S. L. (2004): “Is a theory of total factor productivity really needed?”. En Metroeconómica 58:1 (2007), 195-229, rev. febrero de 2005 y publicada en 2007.

__________________________________ (2005):”La Función agregada en Retrospectiva”. Estudios de Economía Aplicada, Vol.LXIV, No.253 (Julio-Septiembre): pp.43-88.
___________________________________ (2012): “Problems with regional production functions and estimates of agglomeration economies: A caveat emptor for regional scientists”. En Levy Economics Institute of Bard College, Working Paper 725, may.

Felipe, Jesus y Fisher, Franklin M. (2005): “Aggregate production functions, neoclassical growth model and the aggregation problem”. En Estudios de Economía Aplicada, Vol. 24 -1, 2006, págs. 127-163.

Hayek, F. A. (2007): “Principles of Economic. Introduction”. En Instituto de Estudios Humanos.Los primeros escritos se hicieron en 1871, reproducción en 2007, basada en la edición de 1976. 

Keynes, John Maynard (1936): “Teoría general de la ocupación, el interés y el dinero”. Edit. Fondo de Cultura Económica, octava reimpresión de 194, México.

Marchal, Adré (1955): “Metodologia de la ciencia economica. Los problemas actuales del analisis economico, sus enfoques fundamentales”. Edit. El Ateneo. Impreso en Argentina, Buenos Aires, 1958.

Roll, Eric (1939): “Historia de las doctrina económicas”. Edit. Fondo de Cultura Económica, décima reimpresión, 1978, de la cuarta en inglés.

Shaikh, Anwar (s/f: 343/354): “Leyes de producción y leyes algebraicas: La pseudofuncion de producción”. New School for Social Research, Faculty of New York. Traducing de I. Argemí.

Sraffa, Piero (1939): “Producción de mercancías por medio de mercancías. Preludio a una crítica de la teórica económica”. Escuela de Cambridge. Versión castellana de Luis Ángel Rojo Duque.