1.- INTRODUCCIÓN: LOS BIENES PÚBLICOS
Las principales características que definen a un bien público son dos: por un lado, la imposibilidad de excluir de su disfrute a quien no colabore a su provisión o mantenimiento, y por otro, la ausencia de rivalidad en el consumo, dado que el uso que realice una persona no limita ni disminuye las posibilidades de los demás para hacer uso de ese mismo bien.
Un problema importante que presentan los bienes públicos reside en que, dada la imposibilidad de exclusión descrita, podrá haber individuos que pretendan disfrutar de ese bien sin realizar el pago correspondiente; surge por consiguiente el problema denominado del gorrón o “free-rider”, lo que podría llegar a provocar que esos bienes no se produzcan, o se haga en una cantidad inferior a la que podríamos considerar deseable. En efecto, en un dilema de un bien público, todos los que se beneficiarían de la provisión de un bien público encuentran costoso contribuir, y preferirían que otros pagaran por el bien en su lugar. Si cada uno sigue la estrategia de equilibrio, el bien no será suministrado o será infra-suministrado (Ostrom, 1998).
Marwell y Ames (1979) afirman que el problema del “free-rider” que se plantea en economía se identifica con la situación planteada en el “dilema del prisionero” que se estudia desde la óptica de la psicología, y que no deja de ser en una u otra formulación un problema de acción colectiva. No obstante, en este trabajo, nos cuestionaremos más adelante si el “dilema del prisionero” es la única forma de modelizar el problema del free-rider que se puede presentar en el suministro de los bienes públicos, o si por el contrario pueden existir otro tipo de dilemas sociales1 que en determinadas circunstancias puedan reflejar más fielmente la estructura del problema examinado. La pregunta a la que en este ámbito según Marwell y Ames se ha de dar respuesta sería la de cuándo un grupo actuará para maximizar su interés colectivo cuando ese comportamiento entra en conflicto con la maximización individual de sus intereses a corto plazo. Para intentar darle respuesta realizan experimentos acerca de la provisión de bienes públicos, concluyendo que el tamaño del grupo puede ser un factor relevante en este contexto.
Holt y Laury (1997) también investigan experimentalmente acerca de la provisión voluntaria al suministro de un bien público, prestando especial atención a los efectos que tendrían sobre la actitud de los individuos la introducción de un periodo de comunicación y un cambio en los rendimientos que proporcionaría la inversión en un bien privado alternativo a la contribución al bien público2 .
Por otro lado, ante una situación en la que algunas personas se comporten como “free-riders” en el suministro de un bien público, otras personas que inicialmente tuvieran una predisposición a pagar pueden modificar su actitud si piensan que el número de individuos que muestran dicha disposición será insuficiente como para que se produzca la provisión del bien público, y sus esfuerzos sean baldíos, especialmente en los casos en los que se requiere que sean un número mínimo de personas quienes colaboren a la consecución o el suministro de ese bien público.
Finalmente, según cómo sea la función de producción del bien público, puede haber ocasiones en las que la colaboración de algunos individuos pueda ser innecesaria y redundante, por lo que algunos puedan decidir no cooperar al suministro del bien público.
Vemos por tanto que la dinámica de comportamiento de los grupos, incluido su tamaño; la posibilidad o no de comunicación entre los implicados, las variaciones en los rendimientos de inversiones alternativas, el contagio de los comportamientos no cooperativos y la forma de la función de producción pueden ser algunos de los factores relevantes para que se presente en mayor o menor medida el problema del “free-rider” en el suministro de los bienes públicos.
Una característica interesante, por tanto, que se presenta en los bienes públicos, como acabamos de señalar, es la que hace referencia a las relaciones existentes entre el nivel de recursos aportados a la producción de un determinado bien público por parte de los contribuyentes y el nivel de provisión que se alcance a conseguir de dicho bien público.
Esta relación se conoce como la función de producción (véase Marwell y Oliver, 1993, o Heckathorn, 1996). Aunque las funciones de producción pueden adoptar muy variadas formas, existen cuatro funciones básicas con las que poder modelar las dinámicas más importantes en los dilemas de los bienes públicos, que son las que se muestran a continuación en la figura nº 1. Otras formas de la función de producción no serían más que combinaciones de las aquí presentadas.

Figura nº 1: distintas funciones de producción de bienes públicos en función del número de contribuyentes.

 

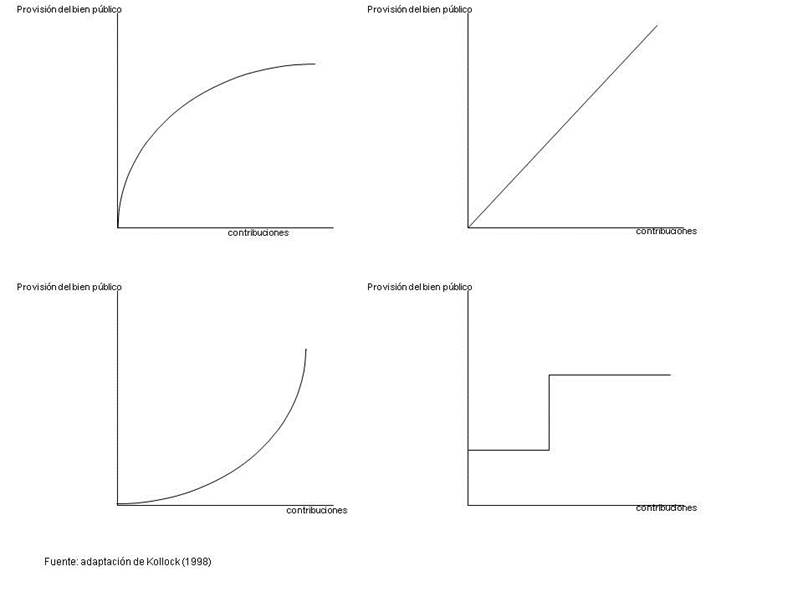
Con una función de producción cóncava, como la del gráfico superior izquierdo, las contribuciones iniciales tienen el mayor efecto, mientras que las siguientes muestran unos rendimientos (entendidos estos como el nivel de provisión del bien público) cada vez menores.
Si la función de producción es lineal, como la del gráfico superior derecho, cada contribución adicional produce un rendimiento constante.
Por otro lado, si la función de producción es convexa, como la del gráfico inferior izquierdo, las primeras contribuciones producen un rendimiento pequeño, mientras que son cada vez mayores cuanto mayor sea el número de contribuciones que se realicen.
Finalmente, en el gráfico inferior derecho podemos apreciar lo que en la literatura se conoce como una función de producción “step-level”, en la que es necesario que se produzca un determinado nivel de contribuciones concreto para que aumente el nivel de provisión del bien público. Si no se alcanza ese nivel, los esfuerzos de los contribuyentes son baldíos.
En la literatura se conoce habitualmente a los juegos en los que existe esta función de producción “step-level” como juegos de minimal contributing set (MCS) es decir, que requieren de un conjunto mínimo de contribuyentes para que se suministren, como se puede apreciar por ejemplo en los trabajos de Van de Kragt, A.; Orbell, J.M. y Dawes, R.M. (1983), Rapoport, A. (1985), Rapoport y Bornstein (1989), Erev y Rapoport (1990).
La contribución de otros individuos por encima de ese nivel puede considerarse redundante e innecesaria hasta que se pueda alcanzar otro nivel, y así sucesivamente.
La obra de referencia para entender la lógica de la acción colectiva es la de Olson (1965). En ella, pone de manifiesto que los individuos miembros de un grupo  grande, si actuaran racionalmente, no harían una contribución voluntaria al suministro de un bien público.
Siempre que en un grupo grande de individuos –o de empresas, Estados, etc.-, haya un interés común en la producción de un bien público, cada uno de ellos se enfrentará a la disyuntiva de contribuir o no. Por el propio hecho de que el grupo es grande, la contribución que cada uno realice habrá de ser necesariamente un porcentaje muy pequeño del total; contribuya o no al suministro del bien público, éste se producirá en una cantidad imperceptiblemente distinta. De ese modo, si no contribuye, podrá disfrutar de él del mismo modo que si lo hiciese.
Por el contrario, si contribuye, y los demás no lo hacen, el bien no se producirá, o solamente se hará en una cantidad prácticamente imperceptible. En ese caso, el esfuerzo de colaborar no se ve recompensado, y lo más racional es no contribuir a producir el bien.
Todd Sandler (1992) dedica todo un libro a la acción colectiva, su teoría y aplicaciones. Comienza el mismo caracterizando el momento en el que surge una situación de acción colectiva, como aquel en que se necesitan los esfuerzos de dos o más individuos para conseguir un resultado. Asimismo, pone como ejemplo de situaciones de acción colectiva a las actividades que implican la mejora del bienestar de un grupo.
El estudio de la acción colectiva se centra para Sandler en el análisis de los factores que llevan a los individuos a coordinar sus actividades para mejorar su bienestar colectivo. Se pregunta, por ejemplo, por qué algunas formas de acción colectiva –como conducir por la derecha- se autoimponen, mientras que otras –como cooperar en una situación de “dilema del prisionero”- no lo hacen. Siguiendo a Olson, examina cómo influyen en ello el tamaño del grupo, su composición, y el diseño institucional.
Russell Hardin (1971) platea que las situaciones de acción colectiva de contribución a un bien colectivo pueden ser plasmadas a través de un “dilema del prisionero”, puesto que el esfuerzo individual para alcanzar su propio interés por parte de los implicados imposibilitará su satisfacción; si el bien colectivo no se proporciona dejarán de percibir un beneficio que sería superior al coste en que incurrirían al ayudar al suministro de ese bien para el grupo.
En el ejemplo numérico que utiliza, supone que se obtienen dos unidades de bien colectivo por cada unidad que pague cada miembro del grupo. Las dos posibles estrategias, por tanto, son contribuir con esa unidad o no. El bien colectivo se reparte equitativamente entre todos los miembros del grupo, independientemente de que hayan decidido colaborar, o no, a su consecución. De este modo, la contribución que realice un miembro del grupo para la consecución del bien colectivo es de sólo una utilidad marginal para sí mismo, mientras que su pago incrementa en casi toda la cantidad que no paga, si es ésta la decisión que toma.
Dado que el beneficio se reparte por igual entre todos, no hay posibilidad de exclusión. Sin embargo, a diferencia de lo que ocurre en los bienes públicos estrictamente considerados, sí que podemos entender que existe rivalidad, dado que el bien colectivo no está en su totalidad a disposición de cada individuo interesado, sino que la parte que disfruta cada uno hace disminuir el total del bien en cuestión.
Como se puede comprobar, este esquema estaría más cercano por tanto a la concepción de la tragedia de los comunes; podemos entender que la aportación que cada cual hace al bien colectivo consiste en el hecho de abstenerse de extraer cantidades del recurso por encima de lo que sería sostenible, redundando este beneficio en el conjunto –donde sí que habrá rivalidad en el uso-, y le supone un coste en el sentido de que deja de ganar por no aprovechar en mayor medida el recurso.
En efecto, la tragedia de los comunes presenta algunas analogías interesantes con el suministro de bienes públicos.
De hecho, como señalan Dawes (1980), Fleishman (1988), Sell y Son (1997) o Apesteguia y Maier-Rigaud (2006), tradicionalmente los bienes públicos y los recursos que pueden verse afectados por la tragedia de los comunes han sido tratados de manera similar. Esto es debido a las similitudes presentes en la matriz de pagos de ambos: en los dos casos, el pago individual por la defección es mayor que el pago por contribuir, del mismo modo que todos los individuos recibirán un pago menor si la cooperación cae por debajo de un determinado porcentaje.
Así, la incapacidad de la exclusión presente en ambos tipos de situaciones, junto con el hecho de que tanto los bienes públicos como los recursos de propiedad común –o libre acceso- se representan a menudo como un dilema del prisionero (Ledyard, 1995; Ostrom, 1995, Gintis, 2000; Camerer 2003; Sandler y Arce, 2003), ha llevado a muchos autores a tratar a ambis dilemas sociales de forma equivalente.
Sin embargo, las diferencias entre ambos tipos de dilemas sociales son perceptibles. En efecto, el libre acceso presente en la tragedia de los comunes se asemeja a la imposibilidad de exclusión que caracteriza a los bienes públicos aunque, por otro lado, la ausencia de rivalidad en el consumo de los bienes públicos choca frontalmente con la rivalidad total en el uso del recurso existente en la tragedia de los comunes, que se plasma en comportamientos guiados por la “regla de captura”.
A pesar de ello, los intereses entre los distintos agentes involucrados en una tragedia de los comunes no están totalmente enfrentados, pues, como ocurre en el dilema del prisionero, puede alcanzarse una situación global mejor si se alcanza una cooperación entre los interesados que si se comportan de modo competitivo, sin cooperar en la conservación del recurso.
Como Sell y Son (1997) señalan, los bienes públicos se crean gracias a contribuciones individuales; la gente debe aportar su dinero –que poseen previamente, y del que pueden disponer de manera individual-, y contribuyen con él al suministro de un bien público.
Ya hemos señalado que en los bienes públicos rige el principio de “no exclusión”, por lo que cada cual va a poder utilizarlo independientemente de cuál haya sido su contribución individual –y cada cual conoce que tendrá ese acceso al bien-. Los recursos naturales objeto de la tragedia de los comunes, en contraste, están ya sujetos al principio de “no exclusión” al encontrarse en un régimen de libre acceso.
En este caso, dado que la gente puede considerar que ya posee el bien, puede ser considerado como parte de la riqueza de la persona –aunque sea poseído igualmente por otros-. En estas circunstancias, por consiguiente, el dilema social gira en torno a restringir el uso del recurso –y no al hecho de aportar a su suministro-.  
La cantidad del recurso disponible depende de cuánto aportan los sujetos implicados –escenario de bienes públicos- o de cuánto dejan de extraer –escenario de tragedia de los comunes-, y también de la forma en la que se relacione este hecho con el nivel de recursos que finalmente esté disponible. En el caso de los recursos sujetos a la tragedia de los comunes, los agentes implicados deben tomar parte del recurso para obtener cualquier beneficio individual, pero el recurso puede degradarse completamente si se utiliza a un ritmo excesivo. Por tanto, el problema en esta situación se centra en utilizarlo moderadamente de forma que el recurso se pueda regenerar y todos puedan seguir disfrutándolo a lo largo del tiempo.
En los dilemas de los bienes públicos, los individuos deben aportar ciertos recursos para obtener un beneficio individual, pero es necesario que se produzcan algunas contribuciones para que el bien público pueda existir. En este sentido, Sell y Son (1997) comparan los bienes públicos con los recursos renovables en régimen de libre acceso, afirmando en el entorno de los dilemas sociales que los problemas de bienes públicos normalmente centran su atención en realizar aportaciones de recursos individuales para crear o mantener un recurso común, mientras que los problemas de recursos de propiedad común y de recursos de libre acceso se centran en las restricciones individuales a extraer del recurso.
Veremos a continuación de qué forma se puede modelizar esquemáticamente la estructura de pagos en la contribución a la producción de un bien público, lo que nos permitirá analizar las relaciones de interdependencia que se establecen entre los individuos interesados por el suministro de un bien público.

2.- MODELIZACIÓN DE LOS BIENES PÚBLICOS
Muchos autores consideran que la situación de interdependencia que se presenta en los bienes públicos responde al planteamiento del “dilema del prisionero” (Marwell y Ames, 1979, Ledyard, 1995; Ostrom, 1990; Gintis, 2000; Camerer, 2003; Sandler y Arce, 2003).

2.1. BIENES PÚBLICOS COMO “DILEMA DEL PRISIONERO”
Parece por tanto oportuno que nos detengamos en el estudio de las características que definen a este juego. El “dilema del prisionero” es un juego en el que hay dos individuos que han de optar entre cooperar o no cooperar, y la mejor elección para cada uno de ellos, independientemente de la estrategia que lleve a cabo el otro, es la de no cooperar –es un equilibrio en estrategias dominantes-.
El equilibrio que alcanzan de ese modo, sin embargo, no es deseable socialmente. De hecho, se podrían producir mejoras paretianas si ambos individuos optaran por cambiar de estrategia y decidiesen cooperar 3. Más aún, la combinación de estrategias no cooperativas arroja el único resultado que no es un óptimo de Pareto.
Los principales motivos por los que ambos individuos tienen esa estrategia dominante no cooperativa en un “dilema del prisionero” son dos: (1) intentar obtener el pago del “gorrón” o free-rider –no cooperando mientras el otro sí que lo hace, aprovechándose de su esfuerzo y obteniendo de esa manera el mejor pago de los disponibles-, y (2) no obtener el pago del “pardillo”, o del incauto, que es aquel que obtiene quien coopera mientras que los demás –en el caso de un juego bipersonal, el otro jugador- no lo hacen, con lo que se recibe el peor pago de los posibles4 .
La estructura de los pagos en un “dilema del prisionero” es la representada en la figura nº2.

Figura nº2: Ordenación de los pagos en un “dilema del prisionero”

donde:
T  > R > C > P.
Las letras utilizadas nos sirven para describir los pagos en los distintos escenarios, de forma que T es el pago de la “tentación” que supone adoptar la estrategia de no cooperar si el otro sí que lo hace; R es la “recompensa” que los dos obtienen por haber tenido ambos jugadores un comportamiento cooperativo; C es el pago de “castigo”, por el hecho de que la estrategia seguida por ambos jugadores es la no cooperativa; y P es el pago del “pardillo”, que es el que percibe el jugador que muestra una actitud cooperativa mientras que es “traicionado” por el otro, que decide no cooperar5 .
En muchas ocasiones, se impone un requisito adicional a la matriz de pagos del “dilema del prisionero”: P + T < 2R; es decir, que la suma de los pagos que obtienen ambos jugadores en una situación en la que uno coopera y el otro no lo hace, ha de ser menor que el pago que obtienen ambos –en conjunto- cooperando.
Este requisito implica que los jugadores no pueden obtener un pago superior al correspondiente a una situación cooperativa llegando, por ejemplo, a un acuerdo en el que uno coopera y el otro no, y después se reparten el pago conjunto –contraviniendo el supuesto de aislamiento o ausencia de información acerca de la estrategia seguida por el otro-.
El Equilibrio de Nash que surge, como fácilmente puede comprobarse analizando los pagos de la representación en forma matricial del juego, es el de la ausencia total de cooperación; la mutua defección. Al tratarse de un Equilibrio de Nash en estrategias dominantes, además, sabemos que es imposible que surja ningún otro Equilibrio de Nash en estrategias mixtas6 .
El dilema se plantea, por consiguiente, debido a que si ambos cooperasen se encontrarían en la mejor situación colectiva, pero existe el miedo a adoptar una estrategia cooperativa y obtener el peor pago como consecuencia de la “traición” del otro, si es que este no actúa de la misma manera.
Como hemos visto, en el dilema del prisionero está presente también, además de ese miedo a la “traición” del otro, la tentación de no cooperar esperando que el otro sí que lo haga, buscando obtener de esa manera el pago del “free rider” o gorrón, que busca aprovecharse del beneficio que supone que el otro coopere, pero sin incurrir él en los costes que supone la cooperación7 .
El Equilibrio de Nash, fruto de la estrategia no cooperativa de ambos jugadores, como dijimos, es ineficiente, pues el pago C es menor que el pago R, y ambos jugadores podrían mejorar por tanto su situación variando sus respectivas estrategias.
En efecto, partiendo de un Equilibrio de Nash no cooperativo, se podría producir una mejora paretiana si ambos individuos decidiesen modificar su estrategia y cooperasen8 . Sin embargo, tratándose de un Equilibrio de Nash, por definición ninguno de ellos tiene incentivos individualmente para realizar dicho cambio –puesto que C > P-.
En esta línea, Elster (1985), citando a Schelling (1978a), define los problemas de acción colectiva –desde una perspectiva fuerte- como aquellos que cumplen dos condiciones: cada individuo obtiene mayores beneficios en condiciones de cooperación universal que en condiciones de defección universal, y cada cual obtiene más beneficios si se abstiene de cooperar, independientemente de lo que hagan los demás.
Una definición más débil, para este autor, consistiría en conservar la primera condición enunciada, sustituyendo la segunda por otras dos: la cooperación es individualmente inestable e individualmente inaccesible. Por individualmente inestable entiende esa situación en la que se tienen incentivos por parte de cada individuo para cambiar de estrategia en una situación de cooperación universal, mientras que por individualmente inaccesible entiende que nadie tiene incentivos para cooperar si se encuentra en una situación de ausencia de cooperación universal.
Aunque conceptualmente presenten diferencias, a efectos prácticos de la formulación como un juego bipersonal, ambas acepciones –fuerte y débil-, no obstante, son equivalentes. En efecto, en la matriz de pagos mostrada en la figura nº 3, en la acepción fuerte, la primera condición implica que se cumpla la desigualdad a > d. La segunda condición supone que c > a y que d > b. De estas tres desigualdades, por tanto, obtenemos una ordenación de los pagos como la siguiente: c > a > d > b.
En la acepción débil, se mantiene la primera condición a > d, y la segunda se sustituye por dos: c > a y d > b. Como se puede apreciar, por tanto, desde un punto de vista práctico de la modelización de las situaciones, ambos enfoques son equivalentes y corresponden como vimos a un “dilema del prisionero” –a diferencia del ejemplo de Sandler (1992) que como veremos más adelante se correspondería con un juego del seguro-.

Figura nº 3: Pagos en una situación de interdependencia estratégica

 

2.2. BIENES PÚBLICOS ENTENDIDOS COMO OTROS DILEMAS SOCIALES
No obstante, aunque la forma habitual de modelizar los dilemas sociales que generan problemas de acción colectiva sea a través del “dilema del prisionero”, no hay una única forma correcta de representar los dilemas sociales, incluidos los problemas en el suministro de bienes públicos; los distintos modelos que se desarrollen dependerán de los supuestos que se realicen acerca de la situación analizada, lo que conducirá a extraer, lógicamente, conclusiones que pueden llegar a ser muy diferentes.
En efecto, partiendo de un “dilema del prisionero”, y modificando ligeramente los valores relativos de los pagos, podemos encontrar dos tipos de juegos diferentes que pueden estar relacionados con la representación de dilemas sociales.
De ese modo, si la mutua cooperación proporciona unos pagos mayores que la defección parcial, estaremos ante un juego de coordinación o seguro. Un error común es considerar que este tipo de juegos no presenta un dilema y lleva de manera inevitable a la mutua cooperación, hecho este que no tendrá lugar en todos los casos, pues dependerá de las expectativas que cada cual tenga respecto de cuál vaya a ser el comportamiento del otro jugador.
En esta línea, Sandler (1992) muestra la situación que se presenta ante la necesidad de contribuir a la financiación de un bien público como un juego entre 2 jugadores, en el que la contribución de ambos genera un beneficio de 10 unidades a cada jugador, y el pago neto es resultado de restar a dicho beneficio la contribución realizada, que ha de ser de 6 unidades.
Si sólo un jugador decide contribuir, incurre en los costes de su contribución, pero el bien público no llega a suministrarse por la ausencia de contribución del otro jugador. La contribución que realiza el jugador que decide cooperar, por tanto, en ese caso, es baldía. Obviamente, quien no contribuye obtiene un pago de cero (y esto es así puesto que no tiene beneficios pero tampoco incurre en costes).
Como podemos apreciar en la figura nº 3, dada la estructura de pagos descrita, existen dos equilibrios de Nash correspondientes a las situaciones en las que ambos individuos adoptan la misma estrategia, siendo el equilibrio cooperativo Pareto-superior respecto del otro.
Figura nº3: Juego bipersonal con cooperación necesaria de ambos jugadores para el suministro de un bien público.

Fuente: Sandler (1992), pág. 39.

Entre otros autores, Runge (1984) muestra cómo el problema del seguro requiere que se desarrollen instituciones económicas y políticas encaminadas a la coordinación de las expectativas para poder superar este tipo de dificultades y acceder a la acción colectiva.
De hecho, en estos juegos la cooperación no es una estrategia dominante, y si un individuo piensa que el otro no va a cooperar, lo mejor que puede hacer es no cooperar tampoco. Esto ocurre porque los juegos de coordinación o seguro, como hemos visto en el ejemplo de Sandler (1992), tienen dos Equilibrios de Nash en estrategias puras, el de la cooperación mutua y el de la mutua defección, siendo el primero el óptimo.
Es importante señalar que entre los incentivos que están presentes en este tipo de juegos y que afectarán a la estrategia que lleven a cabo los jugadores sí que figura el miedo a obtener el pago del “pardillo” como ocurría en el “dilema del prisionero”, pero a diferencia de lo que ocurre en ese juego, no aparece la avaricia que llevaría a intentar explotar al otro (Simpson, 2004).
De hecho, existe una línea de investigación bastante interesante en la que se afirma que pueden producirse procesos de transformación en la forma de concebir estas relaciones de interdependencia, de forma que los implicados en el juego pueden transformar subjetivamente un “dilema del prisionero” en un “dilema del seguro” y tomar sus decisiones de cooperación o defección como si realmente se tratase de este segundo juego, dadas sus expectativas acerca de la actitud cooperativa de los demás (Hayashi et al. 1999, Simpson, 2004).
Otro tipo de juego que podemos obtener mediante la modificación de la ordenación de los pagos del “dilema del prisionero” es el “juego del gallina”. En este juego, la mutua defección proporciona peor pago que la cooperación unilateral, como ocurre a continuación en el ejemplo de la figura nº 4.

 

Figura nº 4: el juego del gallina

 

Donde se cumplen las siguientes desigualdades:
C > A > B > D
X > W > Y > Z

Podríamos interpretar este juego como una situación en la que cada individuo puede producir por separado una renta que beneficiará a ambos, incurriendo para ello en un coste.
Como se puede apreciar, se trata de una situación en la que existen dos equilibrios de Nash en estrategias puras, correspondientes a las combinaciones de estrategias en las que uno coopera y el otro no lo hace.
Partiendo del ejemplo de Sandler de la figura nº 3, variaremos a continuación los pagos para observar en la figura nº 5 una situación con características muy similares a las descritas del “juego del gallina”. En concreto, consideraremos que basta con la aportación de uno de los jugadores para conseguir un bien común.
Supongamos que esa aportación supone un coste de 6 unidades para quien coopere, mientras que los beneficios que genera para ambos son de 10 unidades, siendo suficiente para obtener ese beneficio que únicamente uno de ellos realice la aportación. En ese caso, la matriz de pagos quedaría como podemos ver en la figura nº 5.

Figura nº 5: situación en la que la aportación de un jugador es suficiente para conseguir un bien común.

Como se puede apreciar en la figura nº 5, en esta situación hay dos Equilibrios de Nash, que se corresponden con los casos en los que uno solo de los jugadores adopta la estrategia cooperativa, obteniéndose en conjunto de esta forma una mejor situación colectiva que si ambos cooperasen.
Aunque la mutua cooperación es la meta clara tanto para el “dilema del prisionero” como para el juego de coordinación, esto no necesariamente se cumple para el “juego del gallina”; si una persona puede producir ese beneficio común, no tiene sentido que el otro duplique los esfuerzos. En efecto, en este tipo de situaciones, los equilibrios de Nash en estrategias puras del juego bipersonal se producen en aquellas situaciones en las que uno de ellos coopera y el otro no lo hace.
Un claro ejemplo de las pequeñas modificaciones que se precisan para obtener distintas estructuras de juegos que muestren distintos dilemas sociales es la siguiente, extraída del trabajo de Simpson (2003):

Figura nº 6: Matrices de pagos para tres dilemas sociales

Dilema del prisionero (miedo y avaricia)

T = 4 > R = 3 > P = 2 > S = 1

 

Miedo (no avaricia)

T = R = 4 > P = 3 > S = 1

Avaricia (no miedo)

T = 4 > R = 2 > P = S = 1                       

 

3. MODELIZACIÓN DE BIENES PÚBLICOS N-PERSONALES
           
Extrapolando el análisis a un número de jugadores mayor de dos podemos encontrar un juego, muy parecido en su planteamiento al “dilema del prisionero”, que es el llamado “dilema del voluntario”. En este tipo de juego, basta con que una persona se sacrifique por el bien del conjunto para que un determinado bien público sea suministrado, como hemos visto que podíamos interpretar que ocurría en el “juego del gallina”. Sin embargo, como sucede en el “dilema del prisionero”, sigue existiendo una estrategia dominante, la de no cooperar –en este caso, no sacrificarse-, pues en ese caso se goza del bien público pero se han de padecer los costes, siempre y cuando se espere que otro lo haga. En caso contrario, se ha de cooperar pues U-K > 0 (véase la tabla adjunta). Parece más “razonable” quedarse esperando a que sea otro quien se sacrifique... lo que puede llevar a que finalmente nadie lo haga.
Como Diekmann (1985) lo plantea es conforme a la tabla de la figura nº 7, en la que las columnas muestran el número de voluntarios para la aportación de ese bien público a excepción del interesado:

Figura nº 7: Dilema del voluntario en la aportación a un bien público

Fuente: Diekmann (1985)

donde U es la utilidad que proporciona el bien público, K son los costes en los que se ha de incurrir para obtener dicho bien público, C es la estrategia cooperativa y D la defectiva, y se cumple que:
U-K > 0
N ≥ 2
Un ejemplo que pone Diekmann de este tipo de juego, citando a Darley y Latané (1968), es lo que denominan “difusión de responsabilidad”, que sucede cuando se produce un accidente o un crimen. En esas circunstancias, la gente se queda con la conciencia más tranquila si ve que hay alguien que ayuda al o a los afectados –algo que implica unos costes para quien lo realiza-. Así, todo el mundo estaría inclinado a no ayudar esperando que algún otro lo haga.
Este mismo dilema lo plantea Rapoport (1988) con un ejemplo numérico (figura nº 8), en el que considera que el bien público es valorado por los individuos como una utilidad de 10, mientras que el coste en el que incurre cada individuo que voluntariamente coopere es de 5. En este caso, en columnas tenemos el número de personas que son voluntarios para el suministro de ese bien público:

Figura nº 8: Ejemplo numérico del dilema del voluntario

Fuente: Rapoport (1988)

En el “dilema del voluntario” cabe hacer una distinción acerca de si los posibles voluntarios para suministrar el bien público tienen conocimiento o no de si los demás están suministrándolo, es decir, si existe algún otro voluntario. Weesie (1993, 1994), distingue en ese sentido entre un “dilema del voluntario” –que reservaría para la situación en la que hay información incompleta, es decir, se desconoce si existe algún voluntario-, y un “dilema del voluntario coordinado9 ”, en el que sí que se conoce si se presenta algún voluntario.
Una versión más exigente del “dilema del voluntario” es la que proponen Murnigham et al. (1993), en la que el pago del voluntario es mucho menor si coopera que si no lo hace. Por compararlo con el ejemplo de Diekmann anterior, se cumpliría la desigualdad U – K < 0. De hecho, los ejemplos que propone acaban con la muerte del voluntario... En ese sentido, su planteamiento se acerca más al dilema del altruista.
En una situación del dilema del altruista el incentivo a defraudar aumenta a medida que el bien colectivo aumenta de valor. En tal caso, con jugadores que adoptasen posturas egoístas, no surgiría ningún dilema pues nadie optará por cooperar, lo que es tanto individualmente como colectivamente racional. Sin embargo, si los jugadores muestran comportamientos altruistas, todos cooperarán porque es lo que los otros prefieren que se haga. En este caso, el problema que puede surgir es la súper-coordinación.
Así, mientras que un comportamiento egoísta conduce en el “dilema del prisionero” a un resultado colectivamente irracional, lo contrario ocurre en el “dilema del altruista”: el comportamiento altruista conduce a resultados colectivamente irracionales, mientras que el comportamiento egoísta lleva a un resultado óptimo en el sentido de Pareto (Heckathorn, 1991); sería el caso en el que el coste de proporcionar un bien colectivo excede de sus beneficios, por lo que su provisión es colectivamente irracional. Este autor se centra en la interacción entre altruistas, mientras que se puede encontrar la interacción entre un altruista y un explotador en el dilema del samaritano (Buchanan, 1975), o en la obra de Becker (1981).
            Heckathorn (1991) muestra también de qué manera se puede transformar un “dilema del prisionero” en un “dilema del altruista”. Su razonamiento parte de la consideración de los costes que supone el suministro de un bien público, como los dedicados a resolver el problema del free-rider. Lógicamente, estos costes reducen la ganancia neta que genera el bien público (como en la parte inferior izquierda de la figura nº 9). Si esos costes llegan a exceder el valor del bien público, el hecho de producir dicho bien supondría obtener una pérdida neta para el grupo.
En ese caso, el grupo se enfrentaría a un “dilema del altruista” (como el mostrado en la parte central inferior de la figura). Así, los altos costes de la cooperación pueden bastar para convertir un “dilema del prisionero” en un “dilema del altruista”.
            Un “dilema del prisionero”, además, se puede convertir en un “dilema del altruista” de una segunda manera. Para ello, consideraremos que los grupos pueden producir bienes públicos, como aire limpio, protección ante los incendios, y carreteras, en distintos niveles. Por otro lado, muchos bienes, incluidos los bienes públicos, están sujetos a la existencia de una rentabilidad marginal decreciente.
Además, aunque en la producción de esos bienes públicos existen inicialmente economías de escala, a partir de un determinado momento los costes marginales aumentan. Esos cambios en las rentabilidades y los costes marginales son importantes pues implican que, según aumenta el nivel de un bien público, inevitablemente se alcanzará un punto a partir del cual los costes marginales superen a la rentabilidad marginal. En ese punto, el “dilema del prisionero” se transforma en un “dilema del altruista”.

Figura nº 9: Costes de la cooperación y la conversión de un dilema del prisionero en un dilema del altruista

Nota: si el coste es pequeño, -a la izquierda- el dilema del prisionero se mantiene; si aumenta –en el centro-, se convierte en un dilema del altruista; y si lo hace aún más –a la derecha-, es preferible una mezcla de actitudes cooperativas y no cooperativas a la cooperación universal.

Fuente: Adaptación de Heckathorn (1991)

4.- CONCLUSIONES
La forma más habitual en la literatura económica de modelizar el problema del “free-rider” en los bienes públicos es el juego conocido como el “dilema del prisionero”. En efecto, en este juego actúan dos fuerzas que llevan a que los individuos no deseen colaborar: la avaricia (buscando obtener el pago del free-rider) y el miedo (a obtener el pago del pardillo).
Hay muchos factores que pueden influir en la mayor o menor aparición de colaboración en este tipo de situaciones, como el tamaño del grupo, la posibilidad o no de comunicación entre los implicados, las variaciones en los rendimientos de inversiones alternativas, el contagio de los comportamientos no cooperativos y la forma de la función de producción.
En ocasiones, además, se ha comprobado que los individuos afectados por estas interacciones perciben la situación subjetivamente más como un “dilema del seguro” que como un “dilema del prisionero”. De hecho, algunos autores consideran que es este otro tipo de dilema quien caracteriza mejor las relaciones que se presentan en los bienes públicos.
En efecto, las situaciones en las que la aportación de todos los implicados sea imprescindible para la obtención del bien público, y en caso contrario las aportaciones realizadas se perderían, responden más fielmente a la estructura de pagos de un “dilema del seguro”, en el que existen dos equilibrios de Nash en estrategias puras: la mutua cooperación y la total ausencia de cooperación.
Otros tipos de dilemas sociales, como el “juego del gallina”, pueden también representar una situación que se presente en los bienes públicos. Podríamos interpretar este juego como una situación en la que cada individuo puede producir por separado una renta que beneficiará a ambos, incurriendo para ello en un coste. Se trata de una situación en la que existen dos equilibrios de Nash en estrategias puras, correspondientes a las combinaciones de estrategias en las que uno coopera y el otro no lo hace.
En la extrapolación de los dilemas sociales que plasman las interacciones presentes en el suministro de bienes públicos a un número de implicados superior a dos aparecen otros posibles juegos, como el “dilema del voluntario” y el “dilema del altruista”.
Resulta por tanto fundamental identificar no solamente cuál es el dilema social que está presente en cada formulación de un dilema del bien público, sino cómo es percibido este por los ciudadanos si deseamos aplicar las medidas adecuadas para conseguir la cooperación necesaria para superar este tipo de dilemas.

5.- REFERENCIAS BIBLIOGRÁFICAS